A positive charge q is projected in magnetic field of width mv√2qB with velocity v . Then, the time taken by charged particle to emerge from the magnetic field is
m√2qB
πm4qB
πm2qB
nπ√2⋅qB
The correct Answer is:b
To solve the problem of finding the time taken by a charged particle to emerge from a magnetic field, we can follow these steps:
Step 1: Understand the Situation
A positive charge q is projected into a magnetic field with a width d=mv√2qB and with a velocity v. The magnetic field is perpendicular to the velocity of the charge.
Step 2: Determine the Radius of Circular Motion
When a charged particle moves in a magnetic field, it experiences a magnetic force that acts as a centripetal force, causing it to move in a circular path. The radius r of this circular motion can be expressed as:
r=mvqB
Step 3: Compare the Radius and Width
Given that the width of the magnetic field d is less than the radius r (since d=mv√2qB), we can conclude that the particle will not complete a full circular path but will instead trace out a part of a circle.
Step 4: Calculate the Angle Subtended
The angle θ subtended at the center of the circular path when the particle exits the magnetic field can be determined using the sine function:
sin(θ)=dr
Substituting for d and r:
sin(θ)=mv√2qBmvqB=1√2
Thus, we find:
θ=π4
Step 5: Calculate the Time Taken
The time period T for a complete circular motion is given by:
T=2πmqB
Since the particle only travels through an angle of π4, the time t taken to travel through this angle is:
t=θ2π⋅T=π42π⋅2πmqB
Simplifying this gives:
t=mqB⋅14
Final Answer
Thus, the time taken by the charged particle to emerge from the magnetic field is:
t=πm4qB
A positive charge q is projected into a magnetic field with a width d=mv√2qB and with a velocity v. The magnetic field is perpendicular to the velocity of the charge.
When a charged particle moves in a magnetic field, it experiences a magnetic force that acts as a centripetal force, causing it to move in a circular path. The radius r of this circular motion can be expressed as:
r=mvqB
Given that the width of the magnetic field d is less than the radius r (since d=mv√2qB), we can conclude that the particle will not complete a full circular path but will instead trace out a part of a circle.
The angle θ subtended at the center of the circular path when the particle exits the magnetic field can be determined using the sine function:
sin(θ)=dr
Substituting for d and r:
sin(θ)=mv√2qBmvqB=1√2
Thus, we find:
θ=π4
The time period T for a complete circular motion is given by:
T=2πmqB
Since the particle only travels through an angle of π4, the time t taken to travel through this angle is:
t=θ2π⋅T=π42π⋅2πmqB
Simplifying this gives:
t=mqB⋅14
Thus, the time taken by the charged particle to emerge from the magnetic field is:
t=πm4qB
Topper's Solved these Questions
Similar Questions
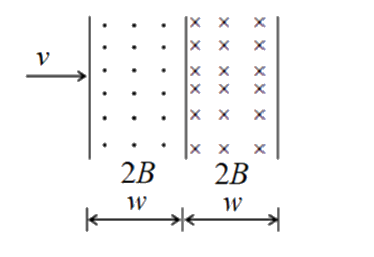
The figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
View SolutionA charge q enters into a magnetic field (B) perpendicularly with velocity V. The time rate of work done by the magnetic force on the charge is
View Solution
Knowledge Check
A positive charge q is projected in magnetic field of width mv√2qB with velocity v as shown in figure. Then time taken by charged particle to emerge from the magnetic field is
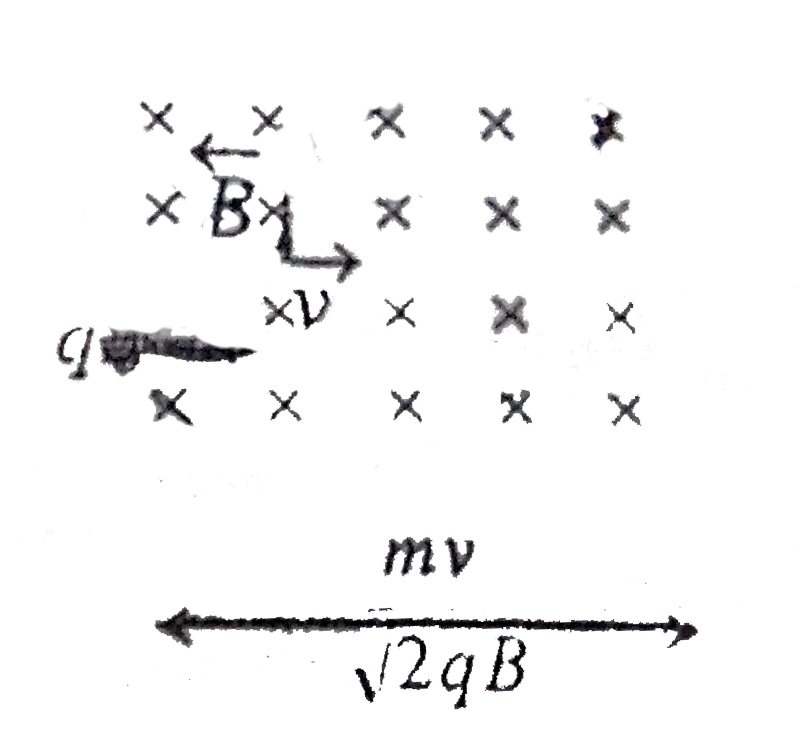 Am√2qBBπm4qBCπm2qBDπm√2qB
Am√2qBBπm4qBCπm2qBDπm√2qBA charged particle is moving with velocity Vin magnetic field
AIts momentum changes but total energy remains sameBboth momentum and total energy remains sameCboth momentum and total energy changeDtotal energy changes but momentum remains the sameA charged particle of mass m and charge q is projected into a uniform magnetic field of induciton →B with speed v which is perpendicular to →B. The width of the magnetic field is d. The impulse imparted to the particle by the field is (d<<mv/qB)
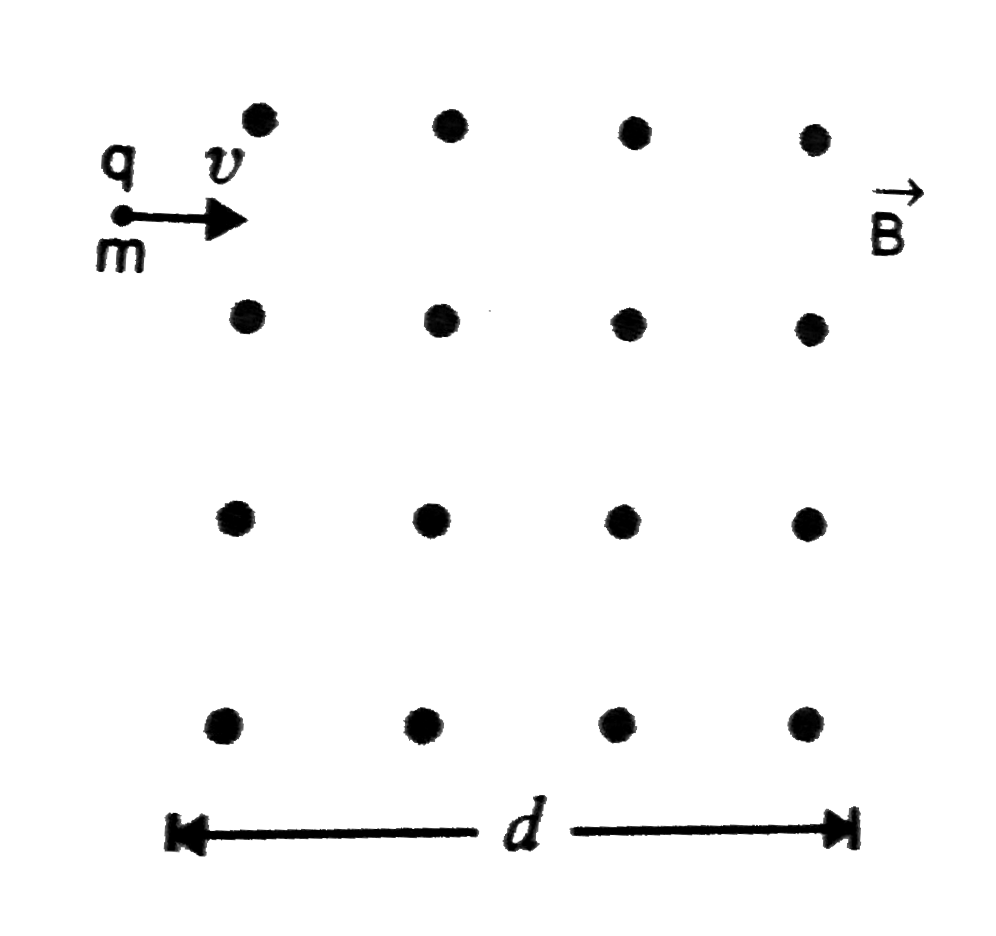 AqBdBqBv/dCmv/(qBd)Dmv2/(qBd)
AqBdBqBv/dCmv/(qBd)Dmv2/(qBd)
Positively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View Solutionthe magnetic field shown in the figure consist of the two magnetic fields.
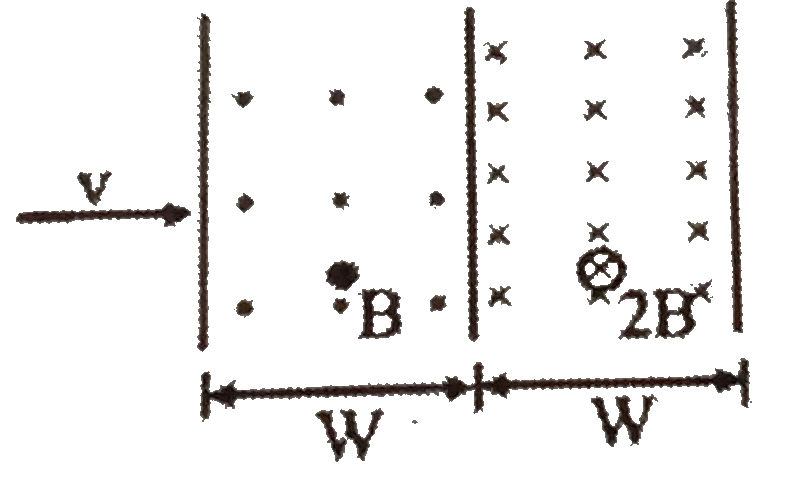
If v is the velocity just required for a charge particles of mass m and charge q to pass through the magnetic field. Particle is projected with velocity 'v' then how much time does such a charge spend in the magntic filed-
View SolutionA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
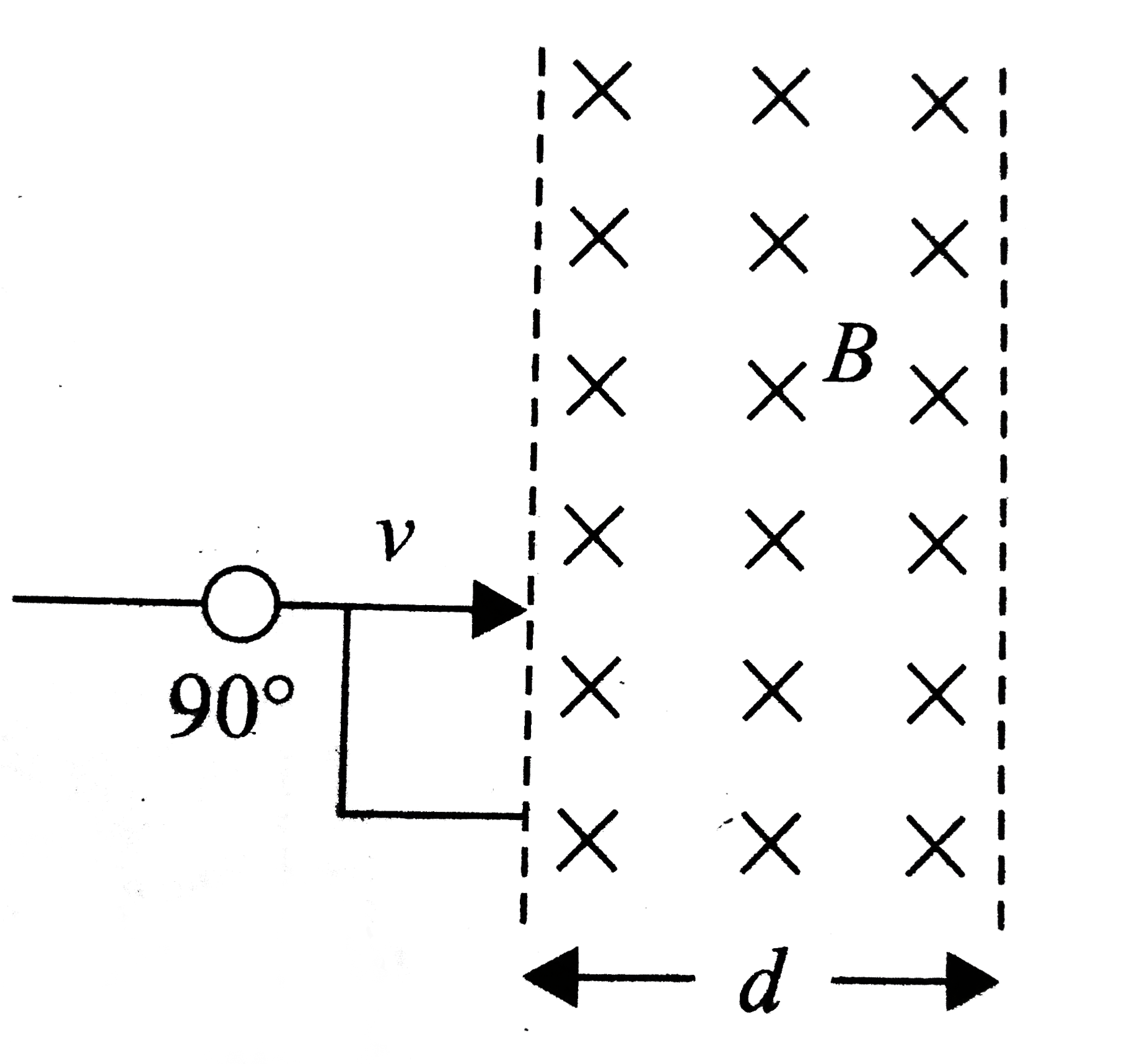
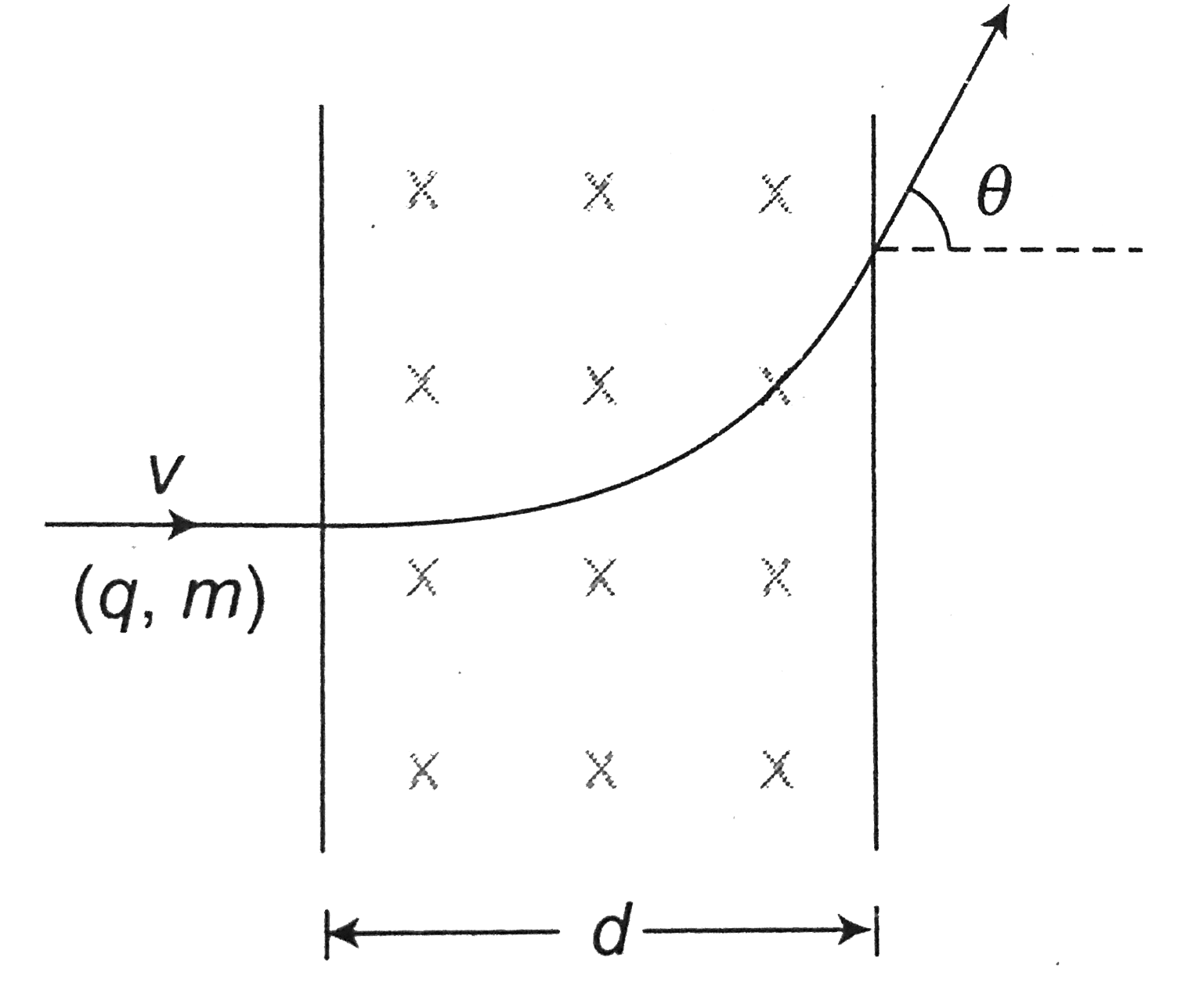
View SolutionA charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. The angle of deviation θ time taken by particle to cross magnetic field will be
View SolutionA charged particle enters in a uniform magnetic field with a certain velocity. The power delivered to the particle by the magnetic field depends on
View Solution
