A positively charged disk is rotated clockwise as shown in Fig. The direction of hte magnetic field at a point A in the plane of the disk is
(1) Let.s think it through qualitatively. Initially, the particle is at rest, so the magnetic force on it is zero and the electric field accelerates the charge in the z direction. As it speeds up, a magnetic force develops which, according to , rotates its velocity vector. The faster it goes, the stronger the magnetic field force

becomes , eventually, it curves the particle back around the y axis. At this point the charge is moving against the electrical force. So it begins to slow down. The magnetic force then decreases, and the electrical force takes over, bringing the charge to rest at point P. There the entire proces commences anew, carrying the particle over to point Q, and so on.
(2) This is a case where we need to apply to decide on the path followed by the charge.
Calculate : There being no force in the x direction, the velocity of the particle at any time t can be described by the vector
→v=vyˆj+vzˆk
By applying the equation of Lorentz force, we get
→F=q[Eˆk+(vyˆj+vzˆk)×Bˆi]
=q(E−vyB)ˆk+qvzBˆj
Treating the y and z components separately, we get
may=qvzB
maz=q(E−vyB)
Let us take
ω=qBm
Then the equation becomes
av=ωvz
az=ω(EB−vy).
By differenting the second and using the first to eliminate ay, we get
d2vzdt2=−ω2vz. This is the familiar equation of simple harmonic motion. Its solution is given by
vz=v0sin(ωt+ϕ)
At t = 0, vz=0. This means that ϕ=0. Substituting this expression of vz in the second equation, we get
vy=EB−v0cos(ωt).
At t = 0, vy is also zero. This means that
v0=EB.
Therefore, we get
vyEB[1−cos(ωt)],
vz=EBsin(ωt).
By integrating these two expressions, we get
y=EωB[ωt−sin(ωt)]
z=EωB[ωt−cos(ωt)]
In this expression, if we let
R=EωB
and eliminate sine and cosine, we find that
(y−Rωt)2+(z−R)2=R2.
This is the equation of a circle of radius R whose center is at (0,Rωt,R). This means that the center travels in y direction at a constant speed of E/B.
The particle moves as though it were a spot on the rim of a wheel, rolling down the y axis at a speed v. This path is called a cycloid.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Check point6videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Problems49videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
Similar Questions
A loop when viewed from top carries on anti-clockwise current as shown. The direction of magnetic field is
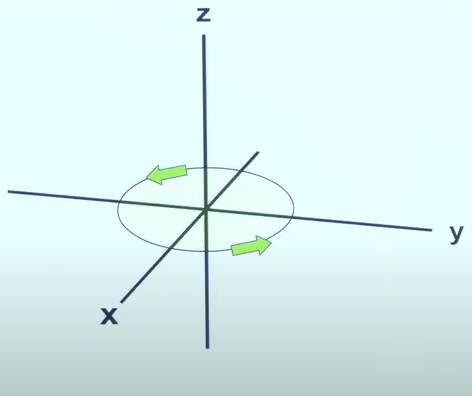 View Solution
View SolutionIf current through a circular coil flows in clockwise direction, then the direction of magnetic field at the centre of the circular coil is………………to the plane of the coil, directed……………. .
View Solution
Knowledge Check
- Question 1 - Select One
Find the magnetic field at the origin in the fig. Shown in fig.
 Aμ0I4R(34ˆk+1πˆj)Bμ0I4R(32ˆk+1πˆj)Cμ0I4R(34ˆk+12πˆj)DNone of these
Aμ0I4R(34ˆk+1πˆj)Bμ0I4R(32ˆk+1πˆj)Cμ0I4R(34ˆk+12πˆj)DNone of these - Question 2 - Select One
Positively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
AAcceleratedBDeceleratedCDeflectedDNo change in velocity - Question 3 - Select One
A circular disc is rotated along clockwise direction in horizontal plane. The direction of torque is
Ahorizontally right sideBhorizontally left sideCvertically upwardDvertically downwards
At which position of the plane of the rotating coil with the direction of magnetic field the e.m.f induced in the coil is maximum ?
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.
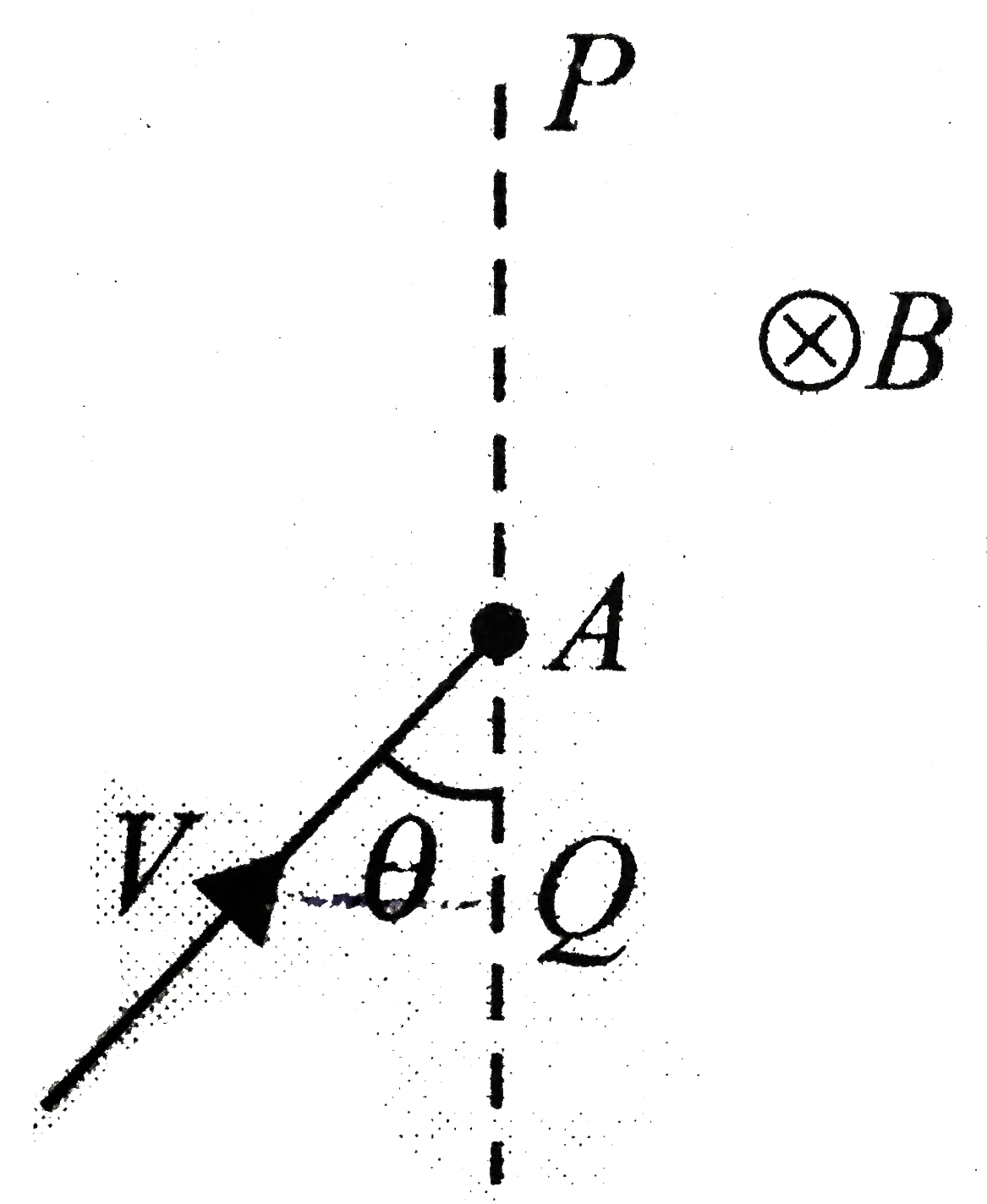 View Solution
View SolutionA current carrying loop is placed in the non-uniform magnetic field whose variation in space is shown in fig. Direction of magnetic field is into the plane of paper. The magnetic of paper. The magnetic force experienced by the loop is
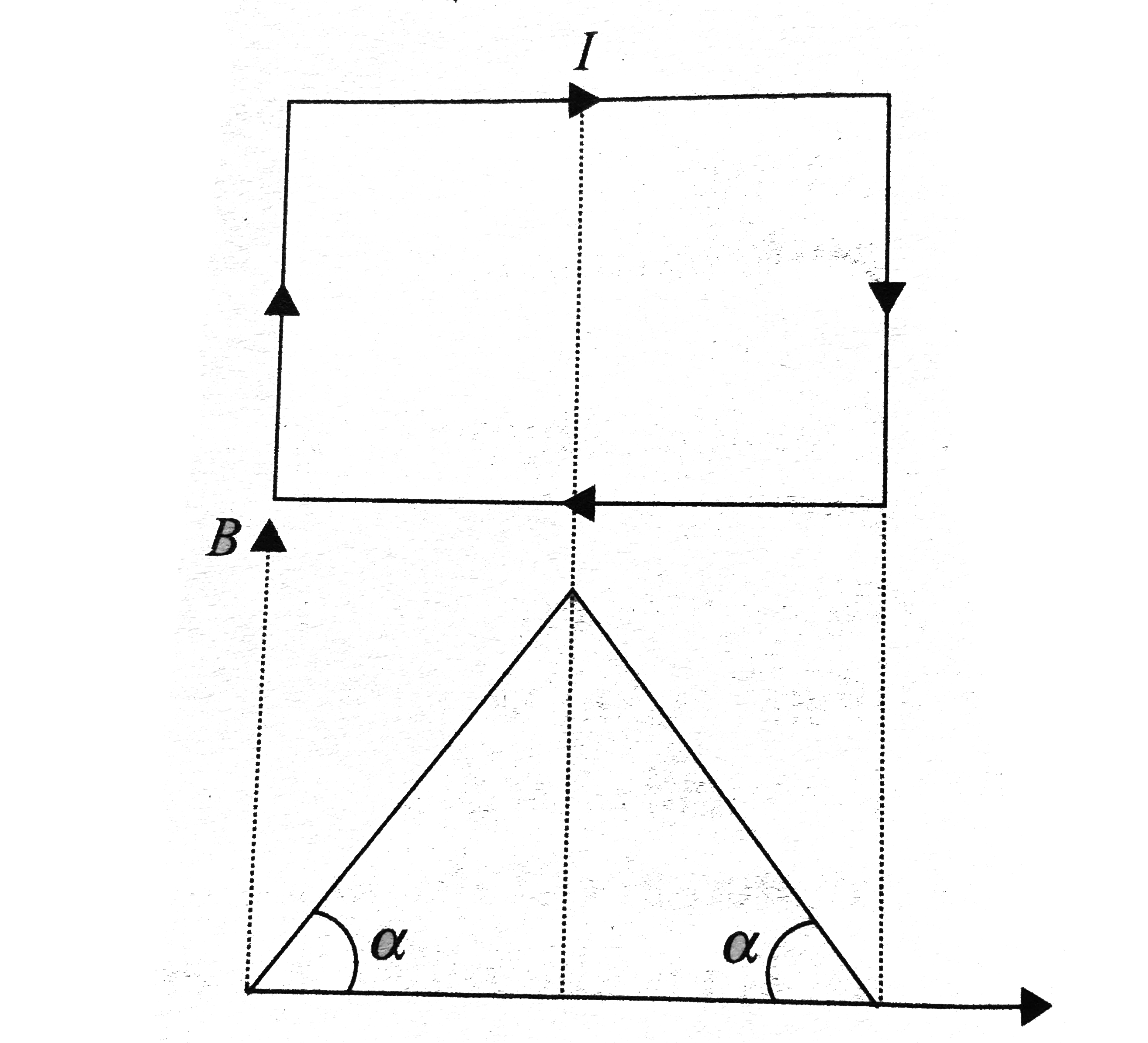 View Solution
View SolutionA positively charged particle projected towards west is deflected towards north by a magnetic field. The direction of the magnetic field is
View SolutionA point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant λ.
The charge in the magnetic dipole moment associated with the orbit. at the end of the time interval of hte magnetic field charge, isView Solution

