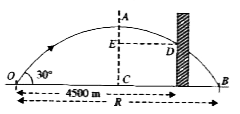
A projectile is fired with a muzzle velocity of 300m/s at an angle of elevation 30∘ above the horizontal, Calculate the height at which it will strike a vertical cliff at a horizontal distance of 4500 m from the point of projection. What will be its velocity when it strikes the cliff ?
Angle of projection θ=30∘
v0=300m/s
Distance of the cliff from the point of projection = 4500m
Horizontal range =R=v20sin2θg=3002sin609.8=7953m
Maximum height attained by the projectile = H
=v20sin2θ2g=3002sin2302×9.8=1147.9m
Let D be the point where the projectile strike the cliff.
The distance ED=45−R2=4500−49532=−523.5m
Horizontal velocity, v0cosθ remains constant
v1=v0cosθ=300×cos30∘=259.8m/s
Time taken to travel the distance ED= Distance ED Horizontal velocity =523.5259.8=2.019s
Downward displacement of the stone from the maximum height A during the time interval 2.01s
=12gt2=12×9.8×2.012=19.8m/s
The height at which the projectile strikes the cliff= Maximum height −19.8
=1147.9−19.8=1128.1m
Vertical component of the velocity of the projectile at the point D
=v2=0+gt=9.8×2.01=19.7m/s
Resultant velocity of the projectile at the point D
=√v21+v22=√259.82+19.72=260.5m/s
Direction of the velocity is given by ϕ, where
tanϕ=v2v1=19.7259.8,ϕ=4.3∘.
The direction of the resultant velocity makes 4.3∘ with direction of the horizontal velocity.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - ADDITIONAL SOLVED PROBLEMS138videos
DYNAMICS
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS20videos
DYNAMICS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems30videos
FRICTION
Similar Questions
A boy throws a ball with a velocity of 15 m/s at an angle of 15° with the horizontal. The distance at which the ball strikes the ground is
View SolutionA projectile shot at an angle of 450 above "the horizontal strikes a building 30m away at a point 15m above the point of projection.The magnitude and direction of velocity of projectile when it strikes the building?
View Solution
Knowledge Check
- Question 1 - Select One
A man throws a ball at an angle of 45∘ with the horizontal plane from a height of 15 m. If the shot strikes the ground at a horizontal distance of 30 in, the velocity of throw is (Take g=10ms−2)
A10 m s−1B10√2ms−1C20ms−1D20√2ms−1 - Question 2 - Select One
A stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
A20 mB25 mC40 mD55m - Question 3 - Select One
A cannon on a level plane is aimed at an angle θ above the horizontal and a shell is fired with a muzzle velocity v0 towards a vertical cliff a distance D away. Then the height from the bottom at which the shell strikes the side walls of the cliff is
ADsinθ−gD22v20sin2θBDcosθ−gD22v20cos2θCDtanθ−gD22v20cos2θDDtanθ−gD22v20sin2θ
A projectile shot at angles of 45∘ above the horizontal strikes a building 30 m away at a point 15 m above the point of projection. Find : (a) the speed of projection . (b) the magnitude and direction of velocity of projectile when it strikes the building .
View SolutionA shell, which is initially located at a distance of 40.4 m above a horizontal plane, is fired horizontally with a muzzle velocity of 285 m/s to strike a target on the horizontal plane. (a) How long does the projectile remain in the air? (b) At what horizontal distance from the firing point does the shell strike the plane? What are the magnitudes of the (c ) horizontal and (d) vertical components of its velocity as it strikes the ground?
View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View SolutionA cannon on a level plane is aimed at an angle α above the horizontal and a shell is fired with a muzzle velocity v0 towards a vertical cliff a distance R away. Then the height from the bottom at which the shell strikes the side walls of the cliff is
View SolutionA projectile is projected from horizontal with velocity (u) making an angle 45∘ with the horizontal direction. Find the distance of the highest point of the projectile from its starting point.
View Solution
