A proton of mass m moving with a speed v0 apporoches a stationary proton that is free to move. Assuming impact parameter to be zero., i.e., head-on collision. How close will be incident proton go to other proton ?
e3πε0m2v0
e3πε0mv0
e2πε0mv20
None of these
The correct Answer is:C
To solve the problem of how close a moving proton can get to a stationary proton during a head-on collision, we can use the principles of conservation of energy and conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the System
We have two protons:
- Proton 1 (moving) with mass m and initial speed v0.
- Proton 2 (stationary) with mass m and initial speed 0.
Since the impact parameter is zero, we can treat this as a head-on collision.
Step 2: Conservation of Momentum
Before the collision, the total momentum of the system is:
pinitial=mv0+0=mv0
After the collision, let V be the common velocity of both protons. Thus, the total momentum after the collision is:
pfinal=(m+m)V=2mV
By conservation of momentum:
mv0=2mV⟹V=v02
Step 3: Conservation of Energy
The initial kinetic energy of the system is:
KEinitial=12mv20
At the closest approach, the kinetic energy will be converted into potential energy due to the electrostatic repulsion between the two protons. The potential energy U at the closest distance R is given by:
U=ke2R
where k is Coulomb's constant and e is the charge of a proton.
At the closest approach, the total energy is the sum of kinetic energy and potential energy:
KEfinal+U=12mv2+ke2R
Substituting V=v02:
KEfinal=2⋅12m(v02)2=12mv204=mv208
Step 4: Set Up the Energy Conservation Equation
Equating initial and final energies:
12mv20=mv208+ke2R
Rearranging gives:
12mv20−mv208=ke2R
4mv208−mv208=ke2R
3mv208=ke2R
Step 5: Solve for R
Rearranging for R:
R=8ke23mv20
Final Answer
The closest distance R that the incident proton can approach the stationary proton is:
R=8ke23mv20
We have two protons:
- Proton 1 (moving) with mass m and initial speed v0.
- Proton 2 (stationary) with mass m and initial speed 0.
Before the collision, the total momentum of the system is:
pinitial=mv0+0=mv0
After the collision, let V be the common velocity of both protons. Thus, the total momentum after the collision is:
pfinal=(m+m)V=2mV
By conservation of momentum:
mv0=2mV⟹V=v02
The initial kinetic energy of the system is:
KEinitial=12mv20
At the closest approach, the kinetic energy will be converted into potential energy due to the electrostatic repulsion between the two protons. The potential energy U at the closest distance R is given by:
U=ke2R
where k is Coulomb's constant and e is the charge of a proton.
KEfinal+U=12mv2+ke2R
Substituting V=v02:
KEfinal=2⋅12m(v02)2=12mv204=mv208
Equating initial and final energies:
12mv20=mv208+ke2R
Rearranging gives:
12mv20−mv208=ke2R
4mv208−mv208=ke2R
3mv208=ke2R
Rearranging for R:
R=8ke23mv20
The closest distance R that the incident proton can approach the stationary proton is:
R=8ke23mv20
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Multiple Correct13videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Linked Comprehension62videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Subject17videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct10videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
Similar Questions
A particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA ball of mass m moving with a speed u0 collides elastically with a rod of mass M suspended in the vertical plane by the hinge O. The rod is free to rotate in the vertical plane. Before and after the collision.
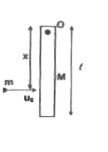 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two objects, one of mass 3 kg and moving with speed of 2 m/s and the other of mass 5 kg and speed 2 m/s, move toward each other and collide head-on. If the collision is perfectly inelastic, find the speed of the object after the collision.
A0.25m/sB0.5m/sC0.75m/sD1m/s - Question 2 - Select One
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 34th of the original. Find the coefficient of restitution.

 View Solution
View SolutionA body of mass m moving with velocity v collides head on with another body of mass 2m which is initially at rest. The ratio of K.E. of colliding body before and after collision will be
View SolutionA particle of mass m1 moves with speed v and collides head on with a stationary particles of mass m2 . The first particle continues to move in the same direction
If m1m2 is (e = coefficient of restitution )View SolutionA neutron moving with a speed v makes a head-on collision with a hydrogen in ground state kept at rest which inelastic collision will be take place is (assume that mass of photon is nearly equal to the mass of neutron)
View SolutionA neutron moving with a speed v makes a head-on collision with a hydrogen in ground state kept at rest which inelastic collision will be take place is (assume that mass of photon is nearly equal to the mass of neutron)
View Solution

