Question

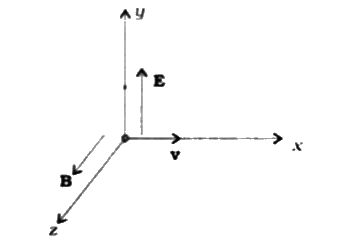
A proton (or charged particle) moving with velocity $v$ is acted upon by electric field $E$ and magnetic field $B$. The proton will move undeflected if

Options

A. E is perpendicular to B
B. E is parallel to v and perpendicular to B
C. E,B and v are mutually perpendicular and v=E/B
D. E and B both are parallel to v

Answer

C

Explanation

To determine the conditions under which a proton (or any charged particle) moving with velocity $$v$$ remains undeflected in the presence of electric field $$E$$ and magnetic field $$B$$, we can follow these steps:

1. Understanding Forces on the Proton:
- The proton experiences two forces: the electric force \( F_E \) due to the electric field \( E \) and the magnetic force \( F_B \) due to the magnetic field \( B \).
- The electric force is given by:
\( F_E = qE \)
where \( q \) is the charge of the proton.
- The magnetic force is given by:
\( F_B = q(v \times B) \)
where \( v \) is the velocity of the proton and \( B \) is the magnetic field.

2. Condition for Undeflected Motion:
- For the proton to move undeflected, the net force acting on it must be zero. This means that the electric force must equal the magnetic force in magnitude but opposite in direction:
\( F_E = F_B \)
- Therefore, we have:
\( qE = q(v \times B) \)

3. Simplifying the Equation:
- Since the charge \( q \) is non-zero (for a proton), we can divide both sides by \( q \):
\( E = vB \)
- This indicates that the electric field \( E \) must be equal to the product of the velocity \( v \) and the magnetic field \( B \).

4. Direction of Fields:
- The directions of the electric field \( E \), magnetic field \( B \), and velocity \( v \) must be such that the forces \( F_E \) and \( F_B \) act in opposite directions. This typically occurs when \( E \) is perpendicular to \( v \) and \( B \) is also perpendicular to \( v \).

5. Final Condition:
- The proton will move undeflected if:
\( E = vB \)
- Additionally, \( E \), \( B \), and \( v \) should be mutually perpendicular.

Conclusion:
The proton will move undeflected if the electric field \( E \) is equal to the product of the velocity \( v \) and the magnetic field \( B \), and all three vectors \( E \), \( B \), and \( v \) are mutually perpendicular.