A radiation of wavelength 200nm is propagating in the form of a parallel surface. The power of the beam is 5mW and its cross-sectional area is 1.0mm2. Find the pressure exerted by radiation on the metallic surface if the radiation is completely reflected.
3.33×10−5
4.33×10−5
5×10−2
None of the above
The correct Answer is:A
To solve the problem of finding the pressure exerted by radiation on a metallic surface when the radiation is completely reflected, we can follow these steps:
Step 1: Calculate the Energy of One Photon
The energy E of a photon can be calculated using the formula:
E=hcλ
where:
- h is Planck's constant (6.626×10−34J s),
- c is the speed of light (3.00×108m/s),
- λ is the wavelength of the radiation (200 nm = 200×10−9m).
Substituting the values:
E=(6.626×10−34J s)(3.00×108m/s)200×10−9m=1.9878×10−25J m200×10−9m=9.939×10−19J
Step 2: Calculate the Number of Photons Incident per Second
The number of photons n incident on the surface per second can be calculated using the formula:
n=PE
where P is the power of the beam (5 mW = 5×10−3W).
Substituting the values:
n=5×10−3W9.939×10−19J≈5.03×1015photons/s
Step 3: Calculate the Change in Momentum per Photon
The momentum p of a photon is given by:
p=hλ
Substituting the values:
p=6.626×10−34J s200×10−9m=3.313×10−24kg m/s
Since the radiation is completely reflected, the change in momentum Δp for each photon is:
Δp=2p=2×3.313×10−24kg m/s=6.626×10−24kg m/s
Step 4: Calculate the Total Change in Momentum per Second
The total change in momentum per second (which is the force F) is given by:
F=n⋅Δp
Substituting the values:
F=(5.03×1015photons/s)⋅(6.626×10−24kg m/s)≈3.33×10−8N
Step 5: Calculate the Pressure Exerted by the Radiation
Pressure P is defined as force per unit area:
P=FA
where A is the cross-sectional area (1.0 mm² = 1.0×10−6m2).
Substituting the values:
P=3.33×10−8N1.0×10−6m2=0.0333N/m2=3.33×10−2Pa
Final Answer
The pressure exerted by the radiation on the metallic surface is approximately:
P≈3.33×10−2Pa
The energy E of a photon can be calculated using the formula:
E=hcλ
where:
- h is Planck's constant (6.626×10−34J s),
- c is the speed of light (3.00×108m/s),
- λ is the wavelength of the radiation (200 nm = 200×10−9m).
E=(6.626×10−34J s)(3.00×108m/s)200×10−9m=1.9878×10−25J m200×10−9m=9.939×10−19J
The number of photons n incident on the surface per second can be calculated using the formula:
n=PE
where P is the power of the beam (5 mW = 5×10−3W).
n=5×10−3W9.939×10−19J≈5.03×1015photons/s
The momentum p of a photon is given by:
p=hλ
Substituting the values:
p=6.626×10−34J s200×10−9m=3.313×10−24kg m/s
Δp=2p=2×3.313×10−24kg m/s=6.626×10−24kg m/s
The total change in momentum per second (which is the force F) is given by:
F=n⋅Δp
Substituting the values:
F=(5.03×1015photons/s)⋅(6.626×10−24kg m/s)≈3.33×10−8N
Pressure P is defined as force per unit area:
P=FA
where A is the cross-sectional area (1.0 mm² = 1.0×10−6m2).
P=3.33×10−8N1.0×10−6m2=0.0333N/m2=3.33×10−2Pa
The pressure exerted by the radiation on the metallic surface is approximately:
P≈3.33×10−2Pa
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Examples
8 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Exercise 3.1
15 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
A beam of light having wavelength 5000Å is incident on a plane metallic surface. The intensity of the incident beam of light is 40wa and its cross-sectional area is 2mm2. What will be pressure (in dyne/cm2) exerted by radiation on the metallic surface if 50% of it is reflected back by metallic surface.
View SolutionA parallel beam of monochromatic light of wavelength 500nm is incident normally on a perfectly absorbing surface. The power through any cross- section of the beam is 10 W. Find (a) the number of photons absorbed per second by the surface and (b) the force exerted by the light beam on the surface.
View SolutionA parellel beam of monochromatic light of wavelength 500 nm is incident normally on a perfectly absorbing surface. The power through any cross section of the beam is 10 W. Find
(a) the number of photons absorbed per second by the surface and
(b) the force exerted by the light beam on the surface.
View SolutionIf a pressure of 378 atm is exerted on a circular cross section of radius 0.1 mm, what is the force exerted on the area?
View SolutionA beam of white light is incident normally on a plane surface absorbing (70%) of the light and reflecting the rest. If the incident beam carries 10 W of power , find the force exerted by it on the surface .
View SolutionRadiation of wavelength 310 nm is incidenton a metal surface of work function 1eV. Find maximum speed of photoelectrons emitted . ( Closed value )
View SolutionRadiation of wavelength 310 nm is incidenton a metal surface of work function 1eV. Find maximum speed of photoelectrons emitted . ( Closed value )
View SolutionWhen radiation of the wavelength λis incident on a metallic surface ,the stopping potential is 4.8 V. If the same surface is illuminated with radiation of double the wavelength ,then the stopping potential becomes 1.6 V.Then the threshold wavelength for the surface is
View SolutionA beam of electromagnetic radiation comprised of wavelength 620 nm on a perfectly absorbing metal (work function, ϕ=2eV) surface of area 1cm2 Pressure exerted by the radiation on the surface is 3×2−13N/cm3 . If one in 3×103photons ejects an electron, and total number of electrons ejected in 1 is 1x, then x is _______
[Given : hc=1240 e Vnm, 1eV=1.6×10−19J]
View Solution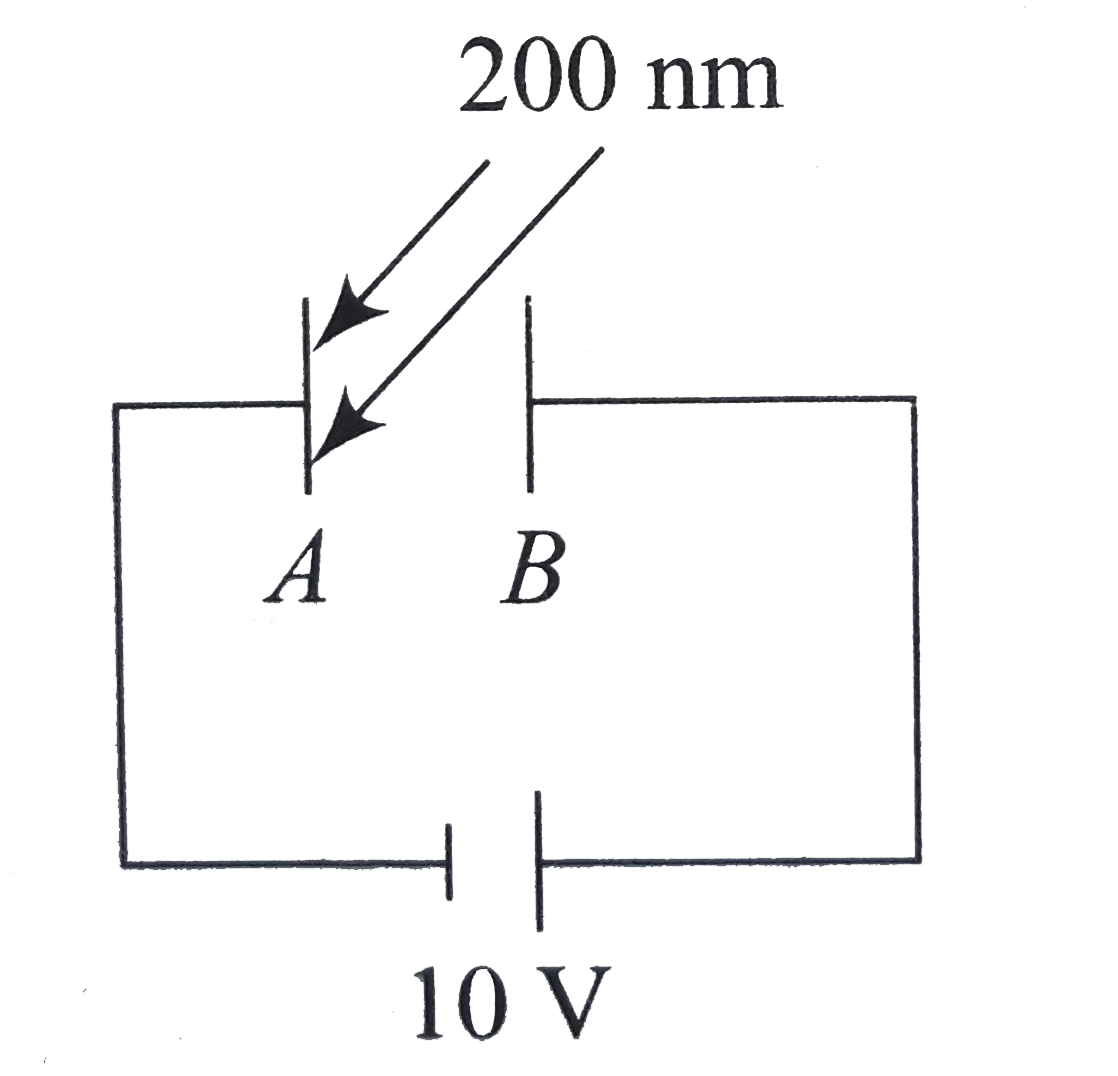
In Fig. electromagnetic radiations of wavelength 200nm are incident on a metallic plate A. the photoelectrons are accelerated by a potential difference of 10 V. These electrons strike another metal plate B from which electromagnetic radiations are emitted. The minimum wavelength of emitted photons is 100nm. If the work function of metal A is found to be (×x10−1)ev, then find the value of x. (Given hc=1240eV nm)
View Solution
