A radioactive isotope is being produced at a constant rate dN/dt=R in an experiment. The isotope has a half-life t1/2.Show that after a time t>>t1/2,the number of active nuclei will become constant. Find the value of this constant.
The correct Answer is:A, B, C
Given Half life period =t12
Rate of Radio active decay
=dNdt=R
⇒R=dNdt
After timet>>t12 the number of active
nuclei will became constant
i.e.(dNdt)present=R=(DNDt)decay
∴R=(DNDt)decay
rArr R=λN
(Whereλ= Radioactive decay constant ,
N= constant number ]
⇒R'=0.693t12(N)
⇒Rt12=0.693N
⇒N=Rt120.693.
Topper's Solved these Questions
- THE NUCLEOUSBOOK - HC VERMA ENGLISHCHAPTER - THE NUCLEOUSEXERCISE - Short answer
12 Videos
- THE NUCLEOUSBOOK - HC VERMA ENGLISHCHAPTER - THE NUCLEOUSEXERCISE - Objective 2
10 Videos
- SPEED OF LIGHTBOOK - HC VERMA ENGLISHCHAPTER - SPEED OF LIGHTEXERCISE - Question for short Answer
5 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Short answer
2 Videos
Similar Questions
A radiaocatice isotope is being produced at a constant rate X. Half-life of the radioactive substance is Y. After some time, the number of radioactive nuceli become constant. The value of this constant is .
View SolutionA rodiactive nucleus is being produced at a constant rate α per second Its decay constant is λ If N0 are the number of nuclie at tieme t=O then, maximum number of nuclei possible are
View Solution
Knowledge Check
Nuclei of a radioactive element A are being produced at a constant rate α. The element has a decay constant λ. At time t=0, there are N0 nuclei of the element.
(a) Calculate the number N of nuclei of A at time t.
(b) If α=2N0λ, calculate the number of nuclei of A after one half-life of A, and also the limiting value of N as t→∞.A1λ[α+(α−N0λ)e−λt]B1λ[α−(α−N0λ)e−λt]Cλ[α−(α−N0λ)e−λt]D[α−(N0λ−α)e−λt]
A radioacitve nucleus is being produced at a constant rate α per second. Its decay constant is λ. If N0 are the number of nuclei at time t=0, then maximum number of nuceli possible are .
View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/2. At the time t=0, there are N0nuclei of the element X.
The number NX of nuclei of X at time t=T1/2 is .
View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/3. At the time t=0, there are N0nuclei of the element X.
The number NY of nuclei of Y at time t is .
View Solution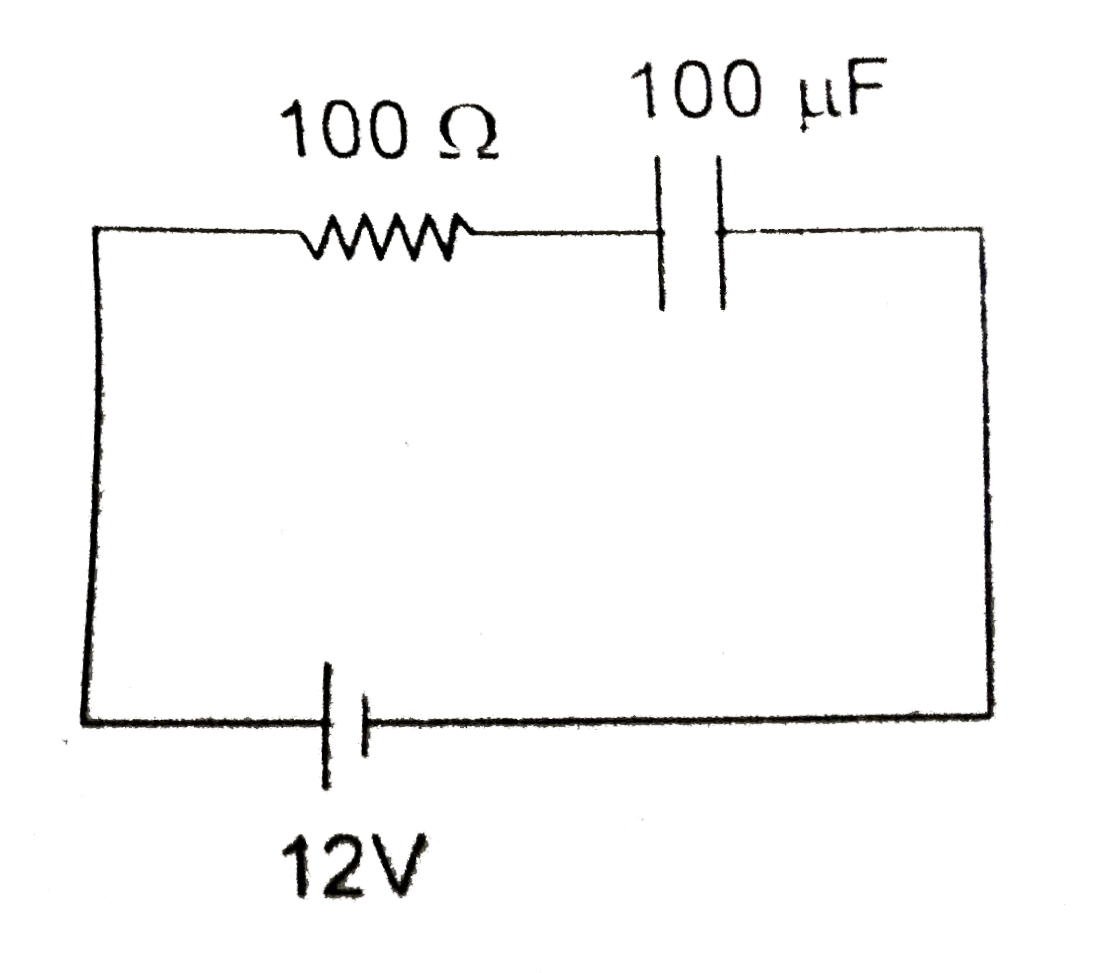
The value of displacement current at t=1 time constant is
View SolutionThalassemia and sickle cell anemia are caued due to problem in globin molecule synthesis . Select the correct statement.
View SolutionNuclei of a radioactive element A are being produced at a constant rate α. The element has a decay constant λ. At time t=0, there are N0 nuclei of the element.
(a) Calculate the number N of nuclei of A at time t.
(b) If α=2N0λ, calculate the number of nuclei of A after one half-life of A, and also the limiting value of N as t→∞.
View SolutionA radioactive substance (A) is produced at a constant rate which decays with a decay constant λ to form stable substance (B).If production of A starts at t=0 . Find (i)The number of nuclei of A and (ii)Number of nuclei of B at any time t.
View Solution
