A railway engine and a car are moving on parallel tracks in opposite directinos with speeds of 144km/hr and 72km/h respectively. The engine is continously sounding a whistle of frequency 500Hz. The velocity of sound in 340ms−1. Calculate the frequency of sound heard in the car when
(i) the car and engineare approaching one another,
(ii) the two are moving away from one another.
To solve the problem, we will use the Doppler effect formula to find the frequency of sound heard in the car when the railway engine and the car are approaching and when they are moving away from each other.
Given Data:
- Frequency of the whistle (source frequency, fs) = 500 Hz
- Speed of sound (v) = 340 m/s
- Speed of the railway engine (vs) = 144 km/h
- Speed of the car (vo) = 72 km/h
Step 1: Convert Speeds from km/h to m/s
1. Convert the speed of the railway engine:
vs=144 km/h=144×1000 m3600 s=40 m/s
2. Convert the speed of the car:
vo=72 km/h=72×1000 m3600 s=20 m/s
Step 2: Calculate Apparent Frequency When Approaching Each Other
When the car and the engine are approaching each other, both the observer (car) and the source (engine) are moving towards each other. Thus, we use the Doppler effect formula:
f′=fs(v+vov−vs)
Where:
- f′ = apparent frequency
- fs = source frequency = 500 Hz
- v = speed of sound = 340 m/s
- vo = speed of the observer (car) = 20 m/s (positive since it is moving towards the source)
- vs = speed of the source (engine) = 40 m/s (positive since it is moving towards the observer)
Substituting the values:
f′=500(340+20340−40)
f′=500(360300)
f′=500×1.2=600 Hz
Step 3: Calculate Apparent Frequency When Moving Away from Each Other
When the car and the engine are moving away from each other, the observer and the source are moving in opposite directions. Thus, we use the same Doppler effect formula:
f′=fs(v−vov+vs)
Where:
- vo = speed of the observer (car) = 20 m/s (negative since it is moving away from the source)
- vs = speed of the source (engine) = 40 m/s (negative since it is moving away from the observer)
Substituting the values:
f′=500(340−20340+40)
f′=500(320380)
f′=500×0.8421≈421.05 Hz
Final Answers:
1. The frequency of sound heard in the car when approaching each other is 600 Hz.
2. The frequency of sound heard in the car when moving away from each other is approximately 421.05 Hz.
- Frequency of the whistle (source frequency, fs) = 500 Hz
- Speed of sound (v) = 340 m/s
- Speed of the railway engine (vs) = 144 km/h
- Speed of the car (vo) = 72 km/h
1. Convert the speed of the railway engine:
vs=144 km/h=144×1000 m3600 s=40 m/s
vo=72 km/h=72×1000 m3600 s=20 m/s
When the car and the engine are approaching each other, both the observer (car) and the source (engine) are moving towards each other. Thus, we use the Doppler effect formula:
f′=fs(v+vov−vs)
Where:
- f′ = apparent frequency
- fs = source frequency = 500 Hz
- v = speed of sound = 340 m/s
- vo = speed of the observer (car) = 20 m/s (positive since it is moving towards the source)
- vs = speed of the source (engine) = 40 m/s (positive since it is moving towards the observer)
f′=500(340+20340−40)
f′=500(360300)
f′=500×1.2=600 Hz
When the car and the engine are moving away from each other, the observer and the source are moving in opposite directions. Thus, we use the same Doppler effect formula:
f′=fs(v−vov+vs)
Where:
- vo = speed of the observer (car) = 20 m/s (negative since it is moving away from the source)
- vs = speed of the source (engine) = 40 m/s (negative since it is moving away from the observer)
f′=500(340−20340+40)
f′=500(320380)
f′=500×0.8421≈421.05 Hz
1. The frequency of sound heard in the car when approaching each other is 600 Hz.
2. The frequency of sound heard in the car when moving away from each other is approximately 421.05 Hz.
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-I
21 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-II
14 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Fill In The Blanks
20 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
A car and bike are moving in opposite directions on parallel tracks with speeds of 72 km/h and 60 km/h respectively. A boy sitting in car is continuously sounding a whistle of frequency 400 Hz. Calculate the frequency of sound heard by person sitting on bike
(a) if car and bike are approaching each other.
(b) if car and bike are moving away from each other.
View SolutionAn engine blowing a whistle of frequency 133 Hz moves with a velocity of 60ms towards a hiss from which an echo is heard. Calculate the frequency of the echo heard by the driver. (velocity of sound in air in 340ms.)
View Solution
Knowledge Check
The driver of a car travelling with speed 30ms−1 towards a hill sounds a horn of frequency 600 Hz. If the velocity of sound in air is 330ms−1, the frequency of reflected sound as heard by driver is
A550HzB555.5HzC720HzD500HzThe driver of a car travelling with a speed of 30 m/s towards a wall sounds a siren of frequency 500 Hz. If the velocity of sound in air is 330 m/s, then the frequency of the sound reflected from the wall and as heard by the driver is
A550 HzB600 HzC650 HzD450 HzAn engine standing at the platform blows a whistle of frequency 305 Hz. If the velocity of sound be 1220 km/h, the frequency of the whistle as heard by a man running towards the engine with a speed of 20 km/s is
A300 HzB305 HzC310 HzD325 Hz
A policeman blows a whistle with a frequency of 500 Hz.A car approaches him with a velocity of 15ms−1.Calculate the change in frequency as heard by the driver of the car as he passes the policeman.Speed of sound in air is 300ms−1.
View SolutionTwo trains are moving towards each other on parallel tracks at speeds of 144kmph and 54kmph. The first train sounds a whistle of frequency 600Hz. Frequency of the whistle as heard by a passenger in the second train is (V=340m/s)
View Solution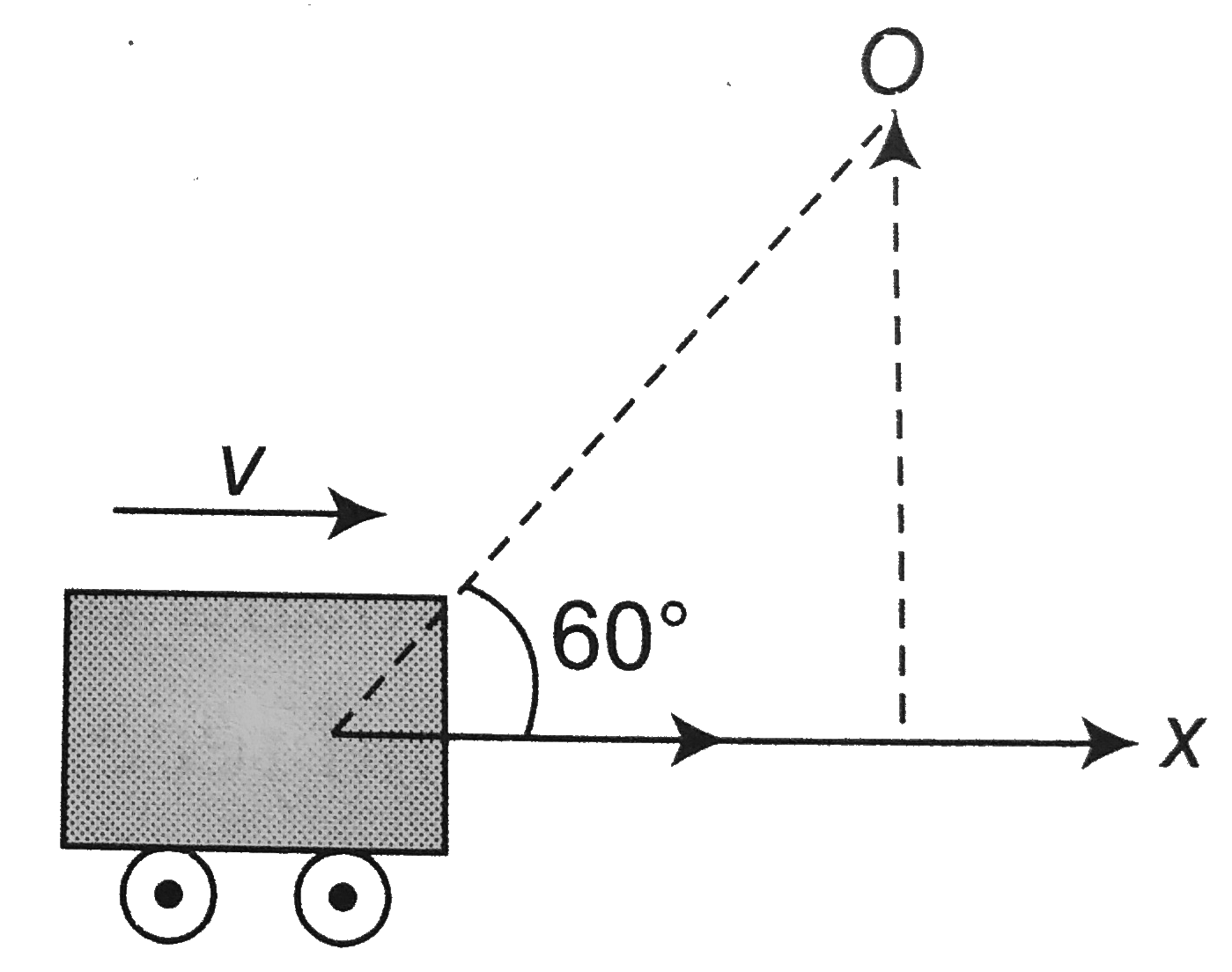
A car is moving along X-axis with a velocity v=20m/s. It sounds a whistle of frequency 660 Hz. If the speed of sound is 340m/s. The apparent frequency heard by the observer O (shown in figure) is:
View SolutionTwo cars moving in opposite directio approach each other with speed of 22m/s and 16.5m/s respectively . The driver of the first car blows a horn having a frequency 400Hz. The frequency heard by the driver of the second car is [ velocity of the sound 340m/s]
View SolutionTwo car moving in opposite directions approach each other with speed of 22m/s and 16.5m/s respectively. The driver of the first car blows a horn having a frequency 400Hz. The frequency heard by the driver of the second car is [velocity of sound 340m/s].
View Solution
