A railway flat car, whose mass together with the artillery gun is , moves at a speed . The gun barrel makes an angle with the horizontal. A shell of mass leaves the barrel at a speed , relative to the barrel. Find the speed of the flat car (in ) in order that it may stop after the firing.
The correct Answer is:2
Using conservation of linear mometum
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - SCQ_TYPE12videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension105videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A railway flatcar whose mass together with the artillery gun is M moves at a speed V along the x-axis
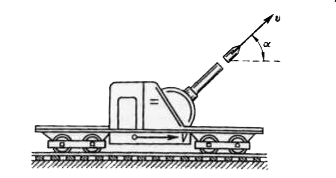
The gun barrel makes an angle a with this axis. A projectile of mass m leaves the gun at speed v (relative to the gun) in the direction of the flatcar's motion. Find the speed of the flatcar after the gun has been fired. What should the speed of the flatcar be for it to stop after the firing? Neglect friction.
Put M = 10 tons, m = 120 kg, V = 6.0 mis, v = 900 m/s, α=30°.View SolutionA car has a gun mounted on it.The combined system has a mass 10m and moves with a velocity v.The barrel of the gun makes an angle 37^(@) with the horizontal.A shell of mass m leaves the barrel at a speed 50m/s relative to barrel in the forward direction.The speed v of the car so that it may stop after the firing is
View Solution
Knowledge Check
- Question 1 - Select One
A railway flat car has an artillery gun installed on it. The combined system has a mass M and moves with a velocity V. The barrel of the gun makes an angle a with the horizontal. A shell of mass m leaves the barrel at a speed v relative to the barrel. The speed of the flat car so that it may stop after the firing is
AmvM+mB(MvM+m)cosαCmvM+m)cosαD(M+m))cosα - Question 2 - Select One
A gun (mass=M) fires a bullet (mass=m) with speed vr relative to barrel of the gun which is inclined at an angle of 60∘ with horizontal. The gun is placed over a smooth horizontal surface. Find the recoil speed of gun.
AV=12mVr(m+M)BV=12mVr(m+M)CV=12mVr(m−M)DNone of these above - Question 3 - Select One
A shell of mass 200g is fired by a gun of mass 100kg. If the muzzle speed of the shell is 80ms−1, then the recoil speed of the gun is
A16cms−1B8cms−1C8ms−1D16ms−1
A car has a gun mounted on it. The combined system has a mass 10m and moves with a velocity V. The barrel of the gun makes an angle 37° with the horizontal. A shell of mass m leaves the barrel at a speed 50 m/s relative to barrel in the forward direction. The speed v of the car so that it may stop after the firing is
View SolutionA shell leaves the barrel of a gun at a speed of 800 m/s. The barrel is 2.0 m long. Find the average acceleration.
View SolutionA gun fires a bullet. The barrel of the gun is inclined at an angle of 45∘ with horizontal. When the bullet leaves the barrel it will be travelling at an angle greater than 45∘ with the horizontal. Is this statement true or false?
View SolutionA gun (mass =M) fires a bullet (mass =m) with speed vr relative to barrel of the gun which is inclined at an angle of 60∘ with horizontal. The gun is placed over a smooth horizontal surface. Find the recoil speed of gun.
 View Solution
View SolutionA canon of mass M is mounted on an east west frictionless railway track. The barrel of cannon faces the north east direction at an angle of 45∘ with the vertical. The canon fires a shot of mass M with a speed V relative to the barrel.
View Solution

