A ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
120∘
90∘
60∘
150∘
The correct Answer is:B
To solve the problem step by step, we will apply Snell's law and the principles of reflection and refraction.
Step 1: Identify the given values
- Angle of incidence (i) = 60°
- Refractive index of glass (n) = √3
Step 2: Apply Snell's Law at the first interface
Using Snell's law:
n1sin(i)=n2sin(r1)
Where:
- n1=1 (refractive index of air)
- n2=√3
- r1 is the angle of refraction at the first interface.
Substituting the values:
1⋅sin(60°)=√3⋅sin(r1)
sin(60°)=√32
Thus,
√32=√3⋅sin(r1)
Dividing both sides by √3:
12=sin(r1)
This gives:
r1=30°
Step 3: Determine the angle of incidence at the second interface
At the second interface (the farther surface of the sphere), the angle of incidence i2 is equal to the angle of refraction r1:
i2=r1=30°
Step 4: Apply Snell's Law at the second interface
Using Snell's law again:
n2sin(i2)=n3sin(r2)
Where:
- n2=√3
- n3=1 (refractive index of air)
- r2 is the angle of refraction at the second interface.
Substituting the values:
√3⋅sin(30°)=1⋅sin(r2)
Since sin(30°)=12:
√3⋅12=sin(r2)
Thus,
sin(r2)=√32
This gives:
r2=60°
Step 5: Determine the angle between the reflected and refracted rays
The angle of reflection (r') at the second interface is equal to the angle of incidence i2:
r′=i2=30°
Now, the angle between the reflected ray and the refracted ray at the second interface can be calculated as:
Angle between reflected and refracted rays=r′+r2
=30°+60°=90°
Final Answer
The angle between the reflected and refracted rays at the surface of the sphere is 90°.
---
- Angle of incidence (i) = 60°
- Refractive index of glass (n) = √3
Using Snell's law:
n1sin(i)=n2sin(r1)
Where:
- n1=1 (refractive index of air)
- n2=√3
- r1 is the angle of refraction at the first interface.
1⋅sin(60°)=√3⋅sin(r1)
sin(60°)=√32
Thus,
√32=√3⋅sin(r1)
Dividing both sides by √3:
12=sin(r1)
This gives:
r1=30°
At the second interface (the farther surface of the sphere), the angle of incidence i2 is equal to the angle of refraction r1:
i2=r1=30°
Using Snell's law again:
n2sin(i2)=n3sin(r2)
Where:
- n2=√3
- n3=1 (refractive index of air)
- r2 is the angle of refraction at the second interface.
√3⋅sin(30°)=1⋅sin(r2)
Since sin(30°)=12:
√3⋅12=sin(r2)
Thus,
sin(r2)=√32
This gives:
r2=60°
The angle of reflection (r') at the second interface is equal to the angle of incidence i2:
r′=i2=30°
Angle between reflected and refracted rays=r′+r2
=30°+60°=90°
The angle between the reflected and refracted rays at the surface of the sphere is 90°.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
A ray incident at an angle of incidence 60∘ enters a glass sphere of μ=√3 and it is reflected and refracted at the farther surface of the sphere. The angle between reflacted and refracted rays at this surface is
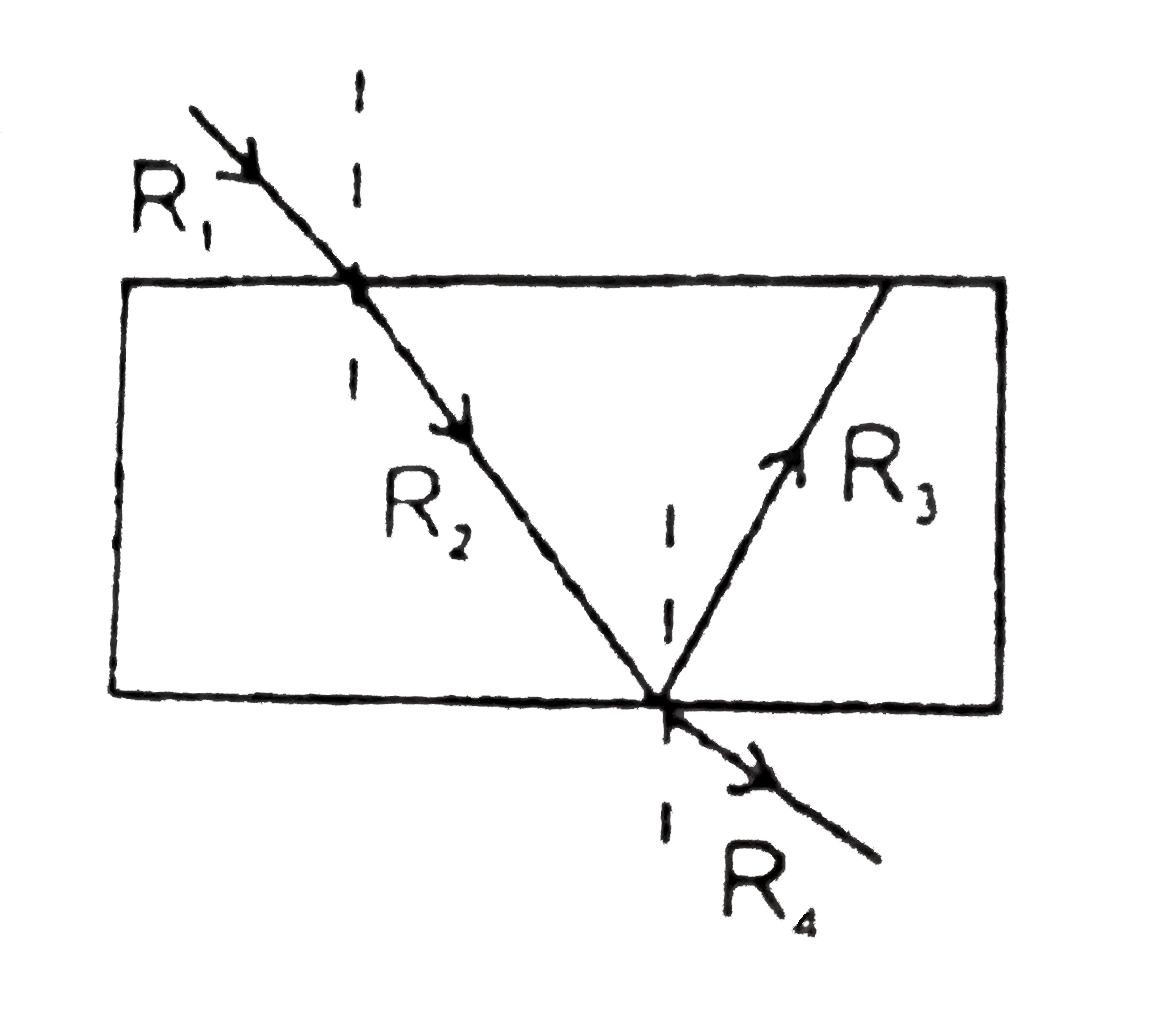
View SolutionA ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :
View Solution
Knowledge Check
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘A ray of light in incident on a glass plate at an angle of 60∘. What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?
A12B√32C32D√3
A ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :

View SolutionA ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
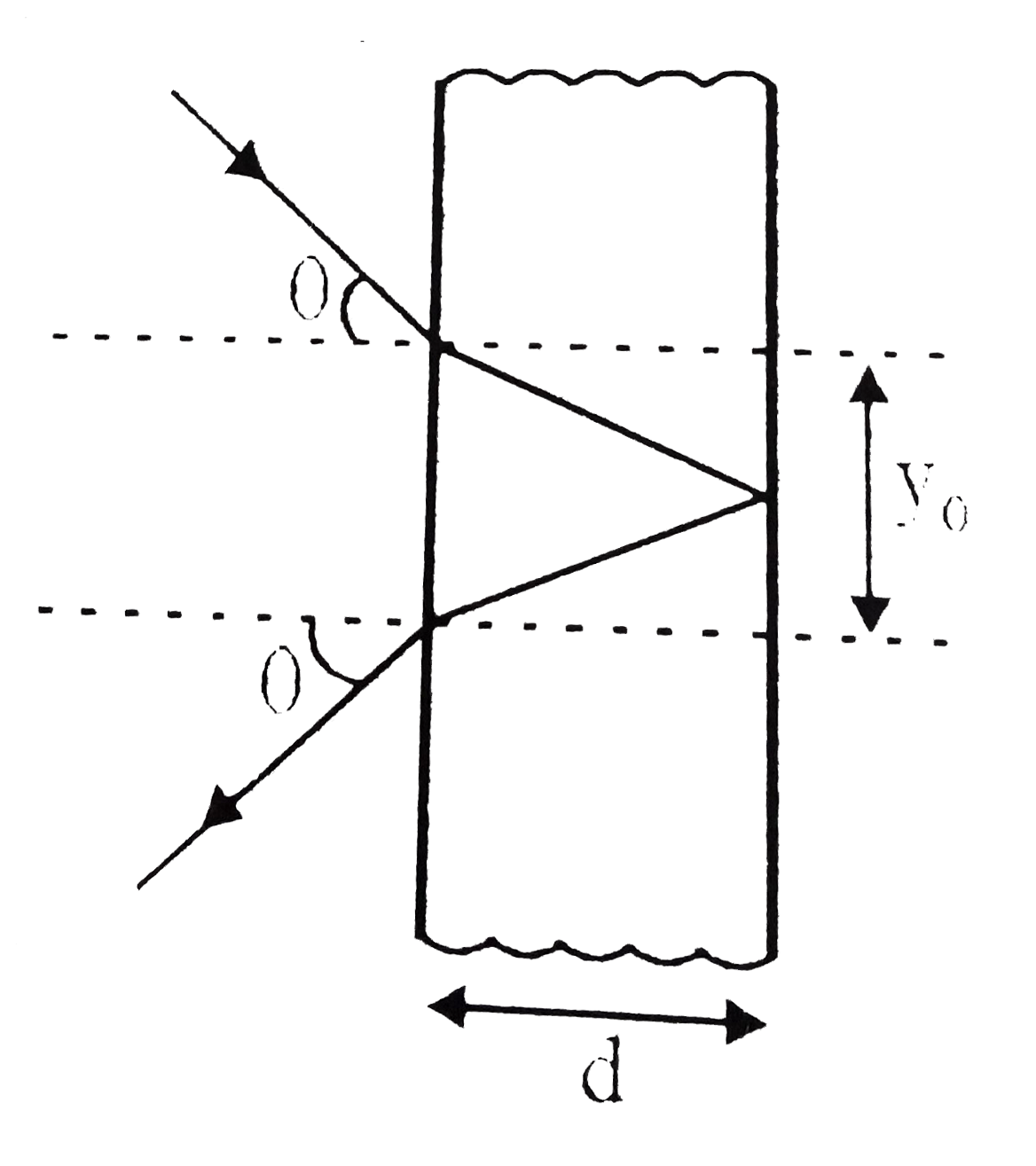
View SolutionA ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View Solution
