A ray of light falls on a normally on a refracting face of a prism. Find the angle of prism if the ray just fails to emerge from the prism (μ=3/2).
The correct Answer is:A, B, C, D
i1=0∘⇒r1=0∘orr2=A
Now, r2=θC=A
∴SinA=sinθC=1μ=23
or A=sin−1(23)
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason
13 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Objective
38 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.7
2 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Aray of light falls on one side of a prism whose refracting angle is 75∘. Find the angle of incidence in order that the emergent ray may just graze the other side, (μ=√2)
View SolutionAn isosceles prism has one of the refracting surfaces silvered. A ray of light is incident normally on the refracting face AB. After two reflections, the ray emerges from the base of the prism perpendicular to it. Find the angle of the prism.
View Solution
Knowledge Check
The angle of incidence for a ray of light at a refracting surface of a prism is 45∘. The angle of prism is 60∘. If the ray suffers minimum deviation through the prism, then the angle of minimum deviation is:
A30∘B60∘C45∘D90∘The angle of incidence for a ray of light at a refracting surface of a prism is 45∘. The angle of prism is 60∘ . If the ray suffers minimum deviation through the prism. The angle of minimum deviation and refractive index of the material of the prism respectively, are
A45∘,√2B30∘,1√2C45∘,1√2D30∘,√2The angle of incidence for a ray of light at a refracting surface of a prism is 45∘. The angle of prism is 60∘. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are :
A45∘,1√2B30∘,√2C45∘,√2D30∘,1√2
A ray of light is incident on an equilateral triangular prism parallel to its base as shown in the figure. The ray just fails to emerge from the face AC. If μ be the refractive index of the prism then the relation(s) is/are :
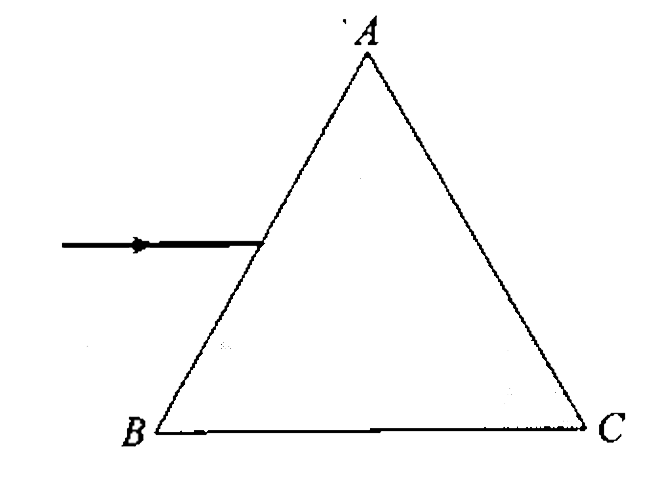
View SolutionThe angle of incidence for a ray of light at a refracting surface of a prism is 45∘. The angle of prism is 60∘. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are :
View SolutionA ray of light is incident on a refracting face of glass prism of refracting angle 30∘. If the ray emerges normally from the second refracting surface, the angle of incidence is refracting surface, the angle of incidence is
[aμg=1.5]
View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
View Solution
