A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘ . Calculate the speed of light through the prism.

The refractive index of the material of the prism,
μ=sinA+δm2sinA2=sin60∘+30∘2sin30∘
[Given,A=60∘,δm=30∘]
=sin45∘sin30∘=1√2×2=√2
Since,μ=cv
∴ v=cμ=2.998×108√2=2.12×108m⋅s−1
∴ speedoflightthroughtheprism=2.12×108m⋅s−1
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - NEET
3 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
Answer the following:
(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘. Calculate the speed of the light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
View Solution(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘. Calculate the speed of the light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.

View Solution
Knowledge Check
If minimum deviation = 30∘, then speed of light in shown prism will be
A3√2×108m/sB1√2×108m/sC2√3×108m/sD2KAε0(K2+1)dA ray of light is incident on an equilateral glass prism placed on a horizontal table. For minimum deviation which of the following is true ?
 APQ is horizontalBQR is horizontalCRS is horizontalDEither PQ or RS is horizontal.
APQ is horizontalBQR is horizontalCRS is horizontalDEither PQ or RS is horizontal.A ray of light is incident on an equilateral glass prism placed on a horizontal table. For minimum deviation which of the following is true:
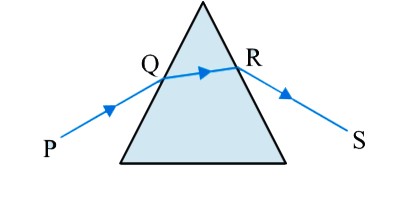 APQ is horizontaBQR is horizontalCRS is horizontalDEither PQ or RS is horizontal
APQ is horizontaBQR is horizontalCRS is horizontalDEither PQ or RS is horizontal
A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 306∘ .Calculate the speed of light through the prism.
View SolutionA ray of incident on an equilateral prism shows minimum deviation of 30∘ .The speed of light through the prism is ?
View SolutionIf minimum deviation = 30∘, then speed of light in shown prism will be
View SolutionA ray of light is incident on an equilateral glass prism placed on a horizontal table. For minimum deviation which of the following is true:

View SolutionA ray of light on passing through an equilateral glass prism, suffers a minimum deviation equal to the angle of the prism. The value of refractive index of the material of the prism is.......
View Solution
