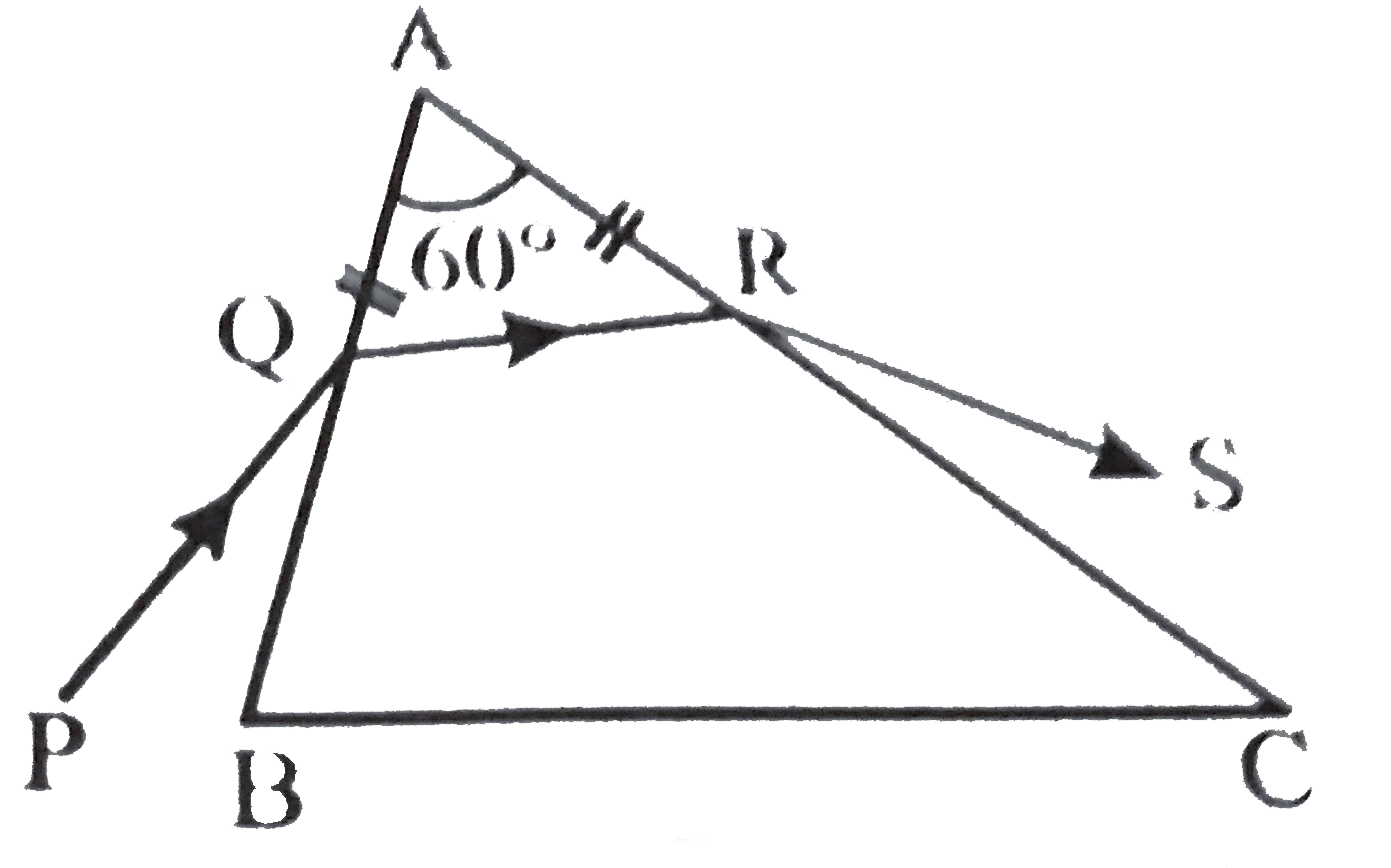
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60∘ and refractive index of material of prism is √3 , calculate angle θ.
The angle of the prism is A=60∘. It is also given that AQ = AR. Therefore, the angles opposite to these two sides are also equal.
Now for the triangle AQR,
∠A+∠AQR+∠ARQ=180∘
∠A+∠AQR+∠ARQ=180∘
∴ r1=r2=30∘[∴∠AQO=∠ARO=90∘]
∴ r1+r2=60∘
When r1andr2 are equal, we have i = e.
Now, according to Snell.s law, μ=sinisinr1
∴ sini=μsinr1=√3sin30∘=√32
∴ i=60∘
Now, the angle of deviation,
θ=i+e−A=60∘+60∘−60∘=60∘

Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - NEET
3 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the meterial of prism is √2 , then the angle of deviation of the ray is
View SolutionA ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the material of prism is 3^1/2, then the angle of deviation of the ray is

View Solution
Knowledge Check
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the material of prism is 3, then the angle of deviation of the ray is
 A60∘B45∘C30∘DNone of the above
A60∘B45∘C30∘DNone of the aboveA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
Asin(A+δ2)sin(A2)BsinAsinδCsinδsinADsin(A+δ)sin(A)A monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
AA<2CBA = 2CCA>2CDA<C2
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle, of prism A = 60∘ and μ of material of prism is then find angle θ .

View SolutionA ray PQ incident on face AB of a prism ABC, as shown in Fig., emerges from the face AC such that AQ=AR. Draw the ray diagram showing the pasage of the ray through the prism. If the angle of prism is 60∘ and refractive index of the material of the prism is √3, determine the values of angle of incidence and angle of deviation.
 .
.
View SolutionThe refracting angle of the prism is 60∘ and the refractive index of the material of the prism is √3. Calculate the angle of minimum deviation in degree.
View SolutionThe refracting angle of the prism is 60∘ and the refractive index of the material of the prism is √3. Calculate the angle of minimum deviation in degree.
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of refracting angle75∘ . It passes through the prism and is incident on the other face at the critical angle If the refracive index of the material of prism is √2, the angle of incidence on the first face o the prism is
View Solution
