A rectangular bar of soap has density 800kg/m3 floats in water density 1000kg/m3. Oil of density 300kg/m3 is slowly added, forming a layer that does not mix with water. When the top surface of thhe oil is the some level as the top surface of the soap. What is the ratio of the oil layer thickness to the soap's thickness. x/L?

37
27
310
38
The correct Answer is:B
Let A be the area of the soap bar.
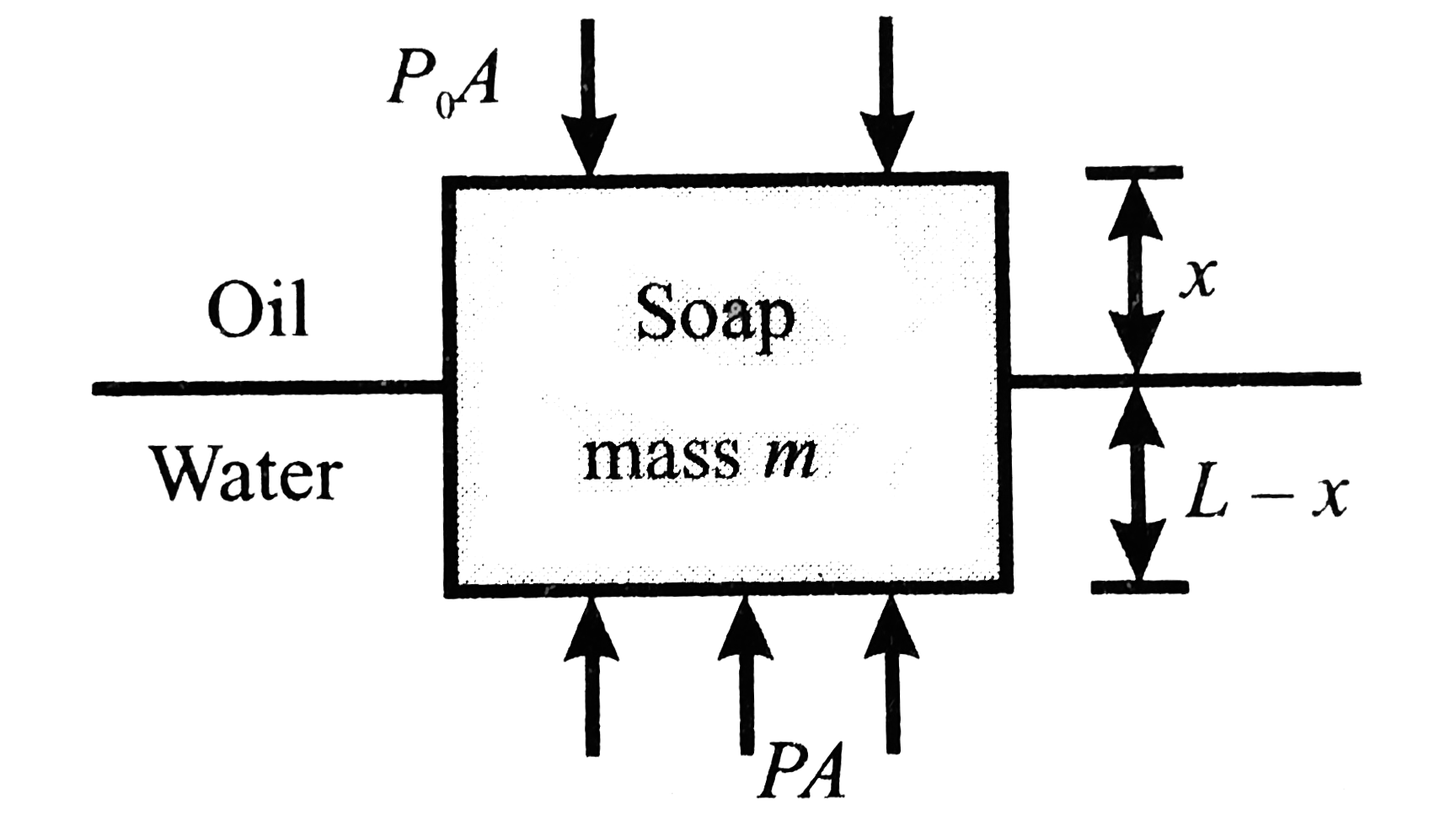
PA−P0A=mg⇒(P−P0)A=mg
⇒[300gx+1000g(L−x)A]=AL800g
⇒xL=27
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
Density of ice is 900kg/m3. A piece of ice is floating in water of density 1000kg/m3. Find the fraction of volume of the picec of ice outside the water.
View SolutionA sample of milk consists of pure milk (density = 1080 kg/m3) diluted with water (density = 1000 kg/m3) and has a density of 1042 kg/m3. Calculate the percentage of water by volume of milk.
View Solution
Knowledge Check
An iceberg of density 900kg/m3 is floating in water of density 1000kg/m3. The percentage of volume of ice cube outside the water is
A20%B35%C10%D25%A tank is filled with water of density 103kg/m3 and oil of density 9×103kg/m3.The height of water layer is 1m and that of the oil layer is 4M. The velocity of efflux front an opening in the bottom of the tank is
A√85m/sB√88m/sC√92m/sD√98m/sA cube of ice of side length 10 cm is floating in water of density 1000 kg/m3. Then pick up the correct statement (density of ice = 900 kg/m3)
A1 cm of the cube will be out of waterB9 cm of the cube will be out of waterC9 cm of the cube will be in waterD1 cm of the cube will be in water
Calculate the molarity of water if its density is 1000kg/m3.
View SolutionCalculate the molarity of water if its density is 1000kg/m3.
View SolutionA solid of density 900kg/m3 floats in oil as shown in the given diagram. The oil floats on water of density 1000kg/m3 as shown.The density of oil in kg/m3 could be:

View SolutionA layer of oil with density 724 kg m−3 floats on water of density 1000kgm−3. A block floats on the oil-water interface with 1/6 of its volume in oil and 5/6 of its volume in water, as shown in the figure. What is the density of the block?

View SolutionThe density of water is 1000kg/m3 and the density of copper is 8900kg/m3. Which of the following statements is incorrect ?
View Solution
