A rectangular block of glass PQRS has a refractive index 1.6 and the critical angle for the glass air interface is 39∘. A pin is placed midway on the face PQ. When observed from the face PS the pin shall

Appear to be near P always
Appear to be at the centre of PS
Appear to be near S
None of these.
The correct Answer is:D
A pin is held at O, mid point of PQ.
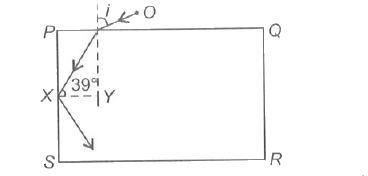
When angle of incidence becomes greater than critical angle, the ray starting from O will undergo total internal reflection and pin shall not be seen at all.
Topper's Solved these Questions
- LIGHT - REFLECTION AND REFRACTIONBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - LIGHT - REFLECTION AND REFRACTIONEXERCISE - ACHIEVERS SECTION (HOTS)
5 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - QUESTIONS
19 Videos
Similar Questions
A rectangular block of glass ABCD has a refractive index 1.6. A pin is placed midway on the face AB, Fig. When observed from the face AD, the pin shall.
 .
.
View SolutionA ray of light travelling in glass having refractive index _(a)μg=3/2 is incident at a critical angle C on the glass air interface. If a thin layer of water is poured on glass air interface, then what will be the angle of emergence of this ray in air when it emerges from water air inteface?
View Solution
Knowledge Check
A rectangular block of glass ABCD has a refractive index 1.6. A pin is placed midway on the faceAB, Fig. When observed from the face AD, the pin shall.
 .Aappear to be near A.Bappear to be near DCappear to be at the centre of ADDnot bee seen at all.
.Aappear to be near A.Bappear to be near DCappear to be at the centre of ADDnot bee seen at all.A cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by
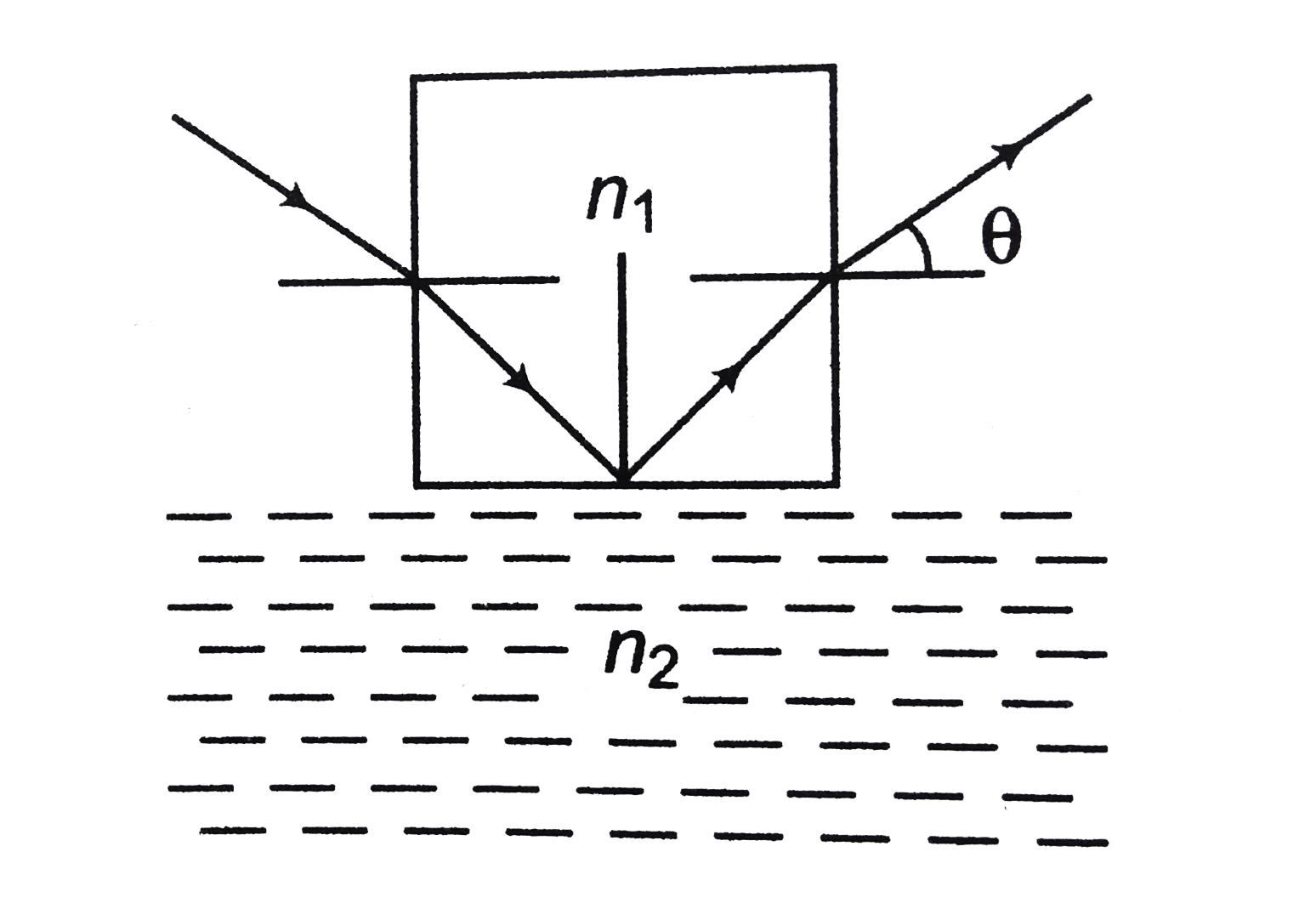 Asinθ<√n21−n22Bcosθ<√n21−n22Csinθ<1√n21−n22Dcosθ<1√n21−n22
Asinθ<√n21−n22Bcosθ<√n21−n22Csinθ<1√n21−n22Dcosθ<1√n21−n22Glass has refractive index μ with respect to air and the critical angle for a ray of light going from glass to air is θ. If a ray of light is incident from air on the glass with angle of incidence θ, the corresponding angle of refraction is
Asin−1(1√μ)B90∘Csin−1(1μ2)Dsin−1(1μ)
A ray of light is incident upon one face of a prism in a direction perpendicular to the other refracting face. The critical angle for glass – air interface is 30°. Find the angle of the prism (assuming it to be less than 90°) if the ray fails to emerge from the other face.
View SolutionA cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by

View SolutionA ray of light travelling inside a rectangular glass block of refractive index√2is incident on the glass-air surface at an angle of incidence of 45∘. The refractive index of air is one. Under these conditions the ray will
View SolutionA ray of light travelling inside a rectangular glass block of refractive index √2 is incident on the glass–air surface at an angle of incidence of 45∘. The refractive index of air is 1. Under these conditions the ray
View SolutionA ray of light travelling inside a rectangular glass of block of refractive indx ×√2 is incident on the glass air surface at an angle of incidence of 45∘ . the refractive index of air is 1 . The ray will
View Solution
