A resistor 'R' and 2(μ)F capacitor in series is connected through a switch to 200 V direct supply. A cross the capacitor is a neon bulb that lights up at 120 V. Calculate the value of R to make the bulb light up 5 s after the switch has been closed. (log102.5=0.4)
1.7×105Ω
2.7×106Ω
3.3×107Ω
1.3×104Ω
The correct Answer is:B
To solve the problem, we need to determine the value of the resistor R that will allow a neon bulb to light up after 5 seconds when connected in series with a 2 µF capacitor across a 200 V supply. The bulb lights up at 120 V.
1. Identify the formula for the voltage across the capacitor:
The voltage V across a charging capacitor in an RC circuit is given by:
V=V0(1−e−tRC)
where:
- V0 is the supply voltage (200 V),
- V is the voltage across the capacitor (120 V),
- t is the time (5 s),
- R is the resistance,
- C is the capacitance (2 µF = 2×10−6 F).
2. Set up the equation using the known values:
Plugging in the values we know:
120=200(1−e−5R⋅2×10−6)
3. Rearranging the equation:
Divide both sides by 200:
120200=1−e−5R⋅2×10−6
Simplifying gives:
0.6=1−e−5R⋅2×10−6
Rearranging further:
e−5R⋅2×10−6=1−0.6=0.4
4. Taking the natural logarithm:
Taking the natural logarithm of both sides:
−5R⋅2×10−6=ln(0.4)
Thus:
5R⋅2×10−6=−ln(0.4)
5. Calculating −ln(0.4):
Using the property of logarithms:
ln(0.4)=ln(2.510)=ln(2.5)−ln(10)
We know from the problem statement that:
log10(2.5)=0.4⟹ln(2.5)=2.303×0.4=0.9212
Therefore:
−ln(0.4)=−ln(2.5)+ln(10)=−0.9212+2.303=1.3812
6. Substituting back to find R:
Substitute −ln(0.4) back into the equation:
5R⋅2×10−6=1.3812
Rearranging gives:
R=51.3812⋅2×10−6=52.7624×10−6≈1.81×106Ω
7. Final result:
Therefore, the value of R is approximately:
R≈1.81MΩ
The voltage V across a charging capacitor in an RC circuit is given by:
V=V0(1−e−tRC)
where:
- V0 is the supply voltage (200 V),
- V is the voltage across the capacitor (120 V),
- t is the time (5 s),
- R is the resistance,
- C is the capacitance (2 µF = 2×10−6 F).
Plugging in the values we know:
120=200(1−e−5R⋅2×10−6)
Divide both sides by 200:
120200=1−e−5R⋅2×10−6
Simplifying gives:
0.6=1−e−5R⋅2×10−6
Rearranging further:
e−5R⋅2×10−6=1−0.6=0.4
Taking the natural logarithm of both sides:
−5R⋅2×10−6=ln(0.4)
Thus:
5R⋅2×10−6=−ln(0.4)
Using the property of logarithms:
ln(0.4)=ln(2.510)=ln(2.5)−ln(10)
We know from the problem statement that:
log10(2.5)=0.4⟹ln(2.5)=2.303×0.4=0.9212
Therefore:
−ln(0.4)=−ln(2.5)+ln(10)=−0.9212+2.303=1.3812
Substitute −ln(0.4) back into the equation:
5R⋅2×10−6=1.3812
Rearranging gives:
R=51.3812⋅2×10−6=52.7624×10−6≈1.81×106Ω
Therefore, the value of R is approximately:
R≈1.81MΩ
Topper's Solved these Questions
Similar Questions
A resistor R and 2μF capacitor in series are connected to a 220V dc supply. Across the capacitor is a neon bulb that strikes at 120V. Calculate the value of R to make the bulb strike 5s after the switch has been closed.
View SolutionAn electric bulb with rating 200 W, 50V is connected to a source of 120 V.
A resistance R is connected in series to the bulb, so that the bulb delivers 200W . Calculate the value of R.
View Solution
Knowledge Check
A resistor R and 2 μF capacitor in series are connected through a 200 V direct supply. Across the capacitor is a neon bulb that lights up at 120 V. Find the value of R to make the bulb light up 5 s after the switch has been closed. (Take log10 2.5=0.4)
A1.7×105ΩB2.7×106ΩC3.3×107ΩD1.3×104ΩFour capacitors of capacitance 10μF and a battery of 200V are arranged as shown. How much charge will flow through AB after the switch S is closed :
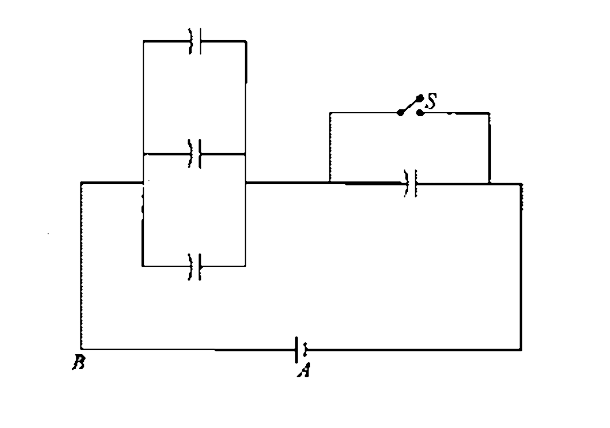A6000μCB4500μCC3000μCD4000μC
A capacitor charged to 10 V is being discharged through a resistance R. At the end of 1 s, the voltage across the capacitor is 5V. What will be the voltage after 2 s?
View SolutionAn inductor of 5 m H is connected in series with a resistor of resistance 4 Ω . A battery of 2 V is connected across the circuit through a switch . Calculate the rate of growth of current just after the switch is on .
View SolutionA bulb with 1.2 ohm resistance is connected to an accumulator in series with a choke. Estimate the inductance of the choke, if the bulb starts to burn brightly 2.5 s after the circuit has been closed.
View SolutionA 60μF capacitor is connected to a 110 V, 60 Hz a.c. supply Determine the r.m.s value of current in the circuit.
View SolutionA capacitor is connected to a 36 V battery through a resistance of 20Ω. It is found that the potential difference across the capacitor rises to 12.0 V in 2μs. Find the capacitance of the capacitor.
View SolutionFour capacitors of capacitance 10μF and a battery of 2V are arranged as shown. How much μC charge will flow through AB after the switch S is closed ?
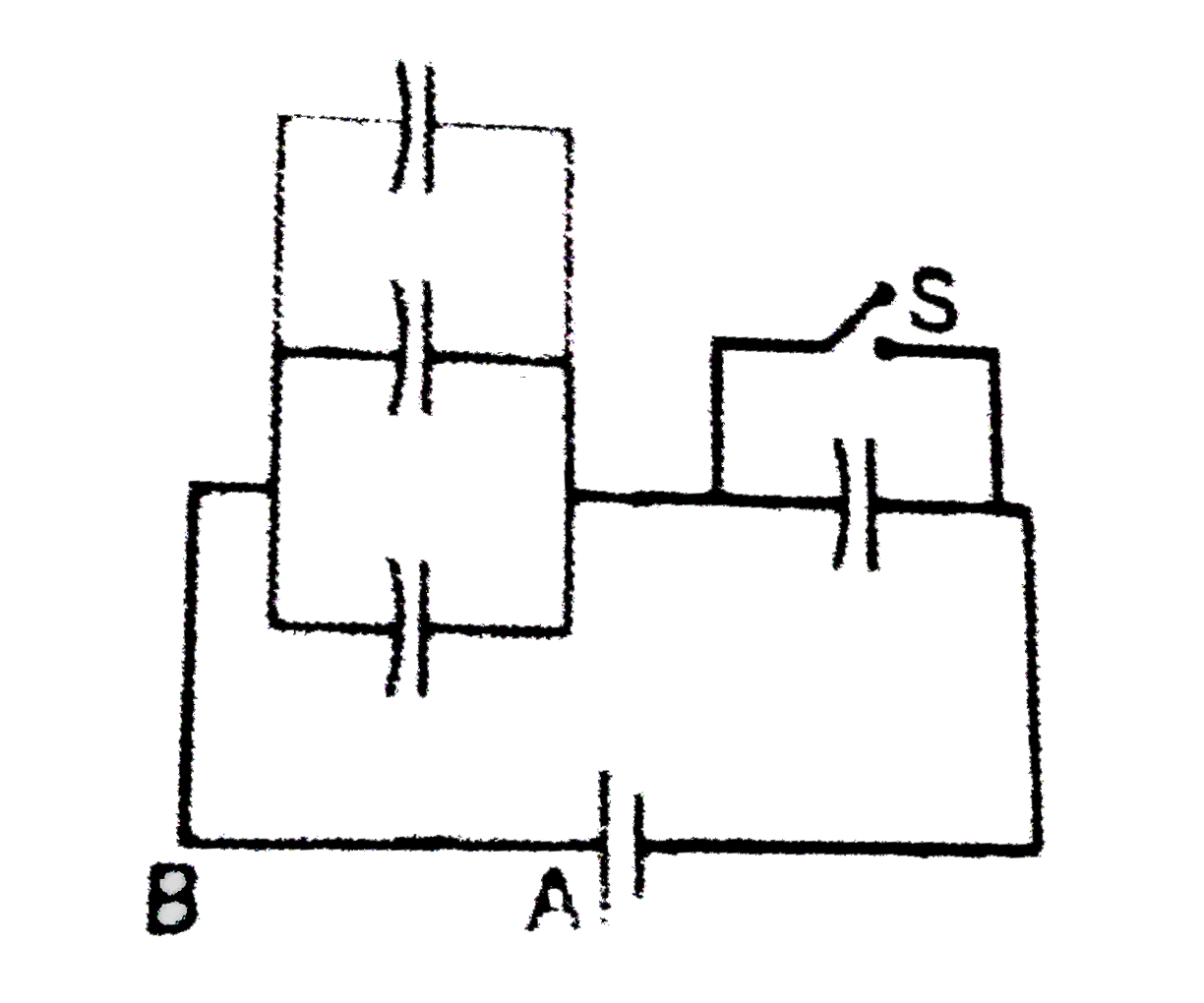
View Solution