A resistor R and the capacitor C are connected in series across an ac source of rms voltage 5V if the rms voltage across C is 3V then that across R is .
1V
2V
3V
4V
The correct Answer is:D
To solve the problem, we need to find the voltage across the resistor R when it is connected in series with a capacitor C across an AC source. Given the RMS voltage across the AC source is 5V and the RMS voltage across the capacitor C is 3V, we can use the following steps:
1. Understand the Circuit Configuration:
- The resistor R and capacitor C are connected in series across an AC source.
- The total RMS voltage VRMS across the series circuit is given as 5V.
- The voltage across the capacitor VC is given as 3V.
2. Use the Voltage Relationship in Series Circuits:
- In a series circuit, the total voltage is the sum of the voltages across each component:
VRMS=VR+VC
- Rearranging this gives us the voltage across the resistor R:
VR=VRMS−VC
3. Substitute the Known Values:
- Substitute VRMS=5V and VC=3V into the equation:
VR=5V−3V
4. Calculate the Voltage Across the Resistor:
- Performing the subtraction:
VR=2V
5. Conclusion:
- The voltage across the resistor R is 2V.
Final Answer:
The voltage across the resistor R is 2V.
- The resistor R and capacitor C are connected in series across an AC source.
- The total RMS voltage VRMS across the series circuit is given as 5V.
- The voltage across the capacitor VC is given as 3V.
- In a series circuit, the total voltage is the sum of the voltages across each component:
VRMS=VR+VC
- Rearranging this gives us the voltage across the resistor R:
VR=VRMS−VC
- Substitute VRMS=5V and VC=3V into the equation:
VR=5V−3V
- Performing the subtraction:
VR=2V
- The voltage across the resistor R is 2V.
The voltage across the resistor R is 2V.
Topper's Solved these Questions
Similar Questions
A resistor and a capacitor are connected in series with an a.c. source. If the potential drop across the capacitor is 5 V and that across resistor is 12 V, applied voltage is
View SolutionAn inductor of negligible resistance and a 50 Ω resistor are connnected in series across an AC supply of 100 V. Calculate the voltage across the inductor if voltage across the resistor is 40 V.
View Solution
Knowledge Check
A resistor an inductor and a capacitor are connected in series to an ac source An ac voltmeter measures the votage across them as 800V,30V and 90V respectively The rms value of the supply voltage is .
A100VB100√2VC200VD200√2VA resistance of 200Ω and capacitor of 15μF are connected in series to a 220 V, 50 Hz AC source. The voltage (rms) across the resistor and capacitor is that
A151 V, 160.4 VB150 V, 100.3 VC220 V, 91.8 VD145 V, 311.3 VA 50HzAC source of 20V is connected across R and C as shown in figureure.
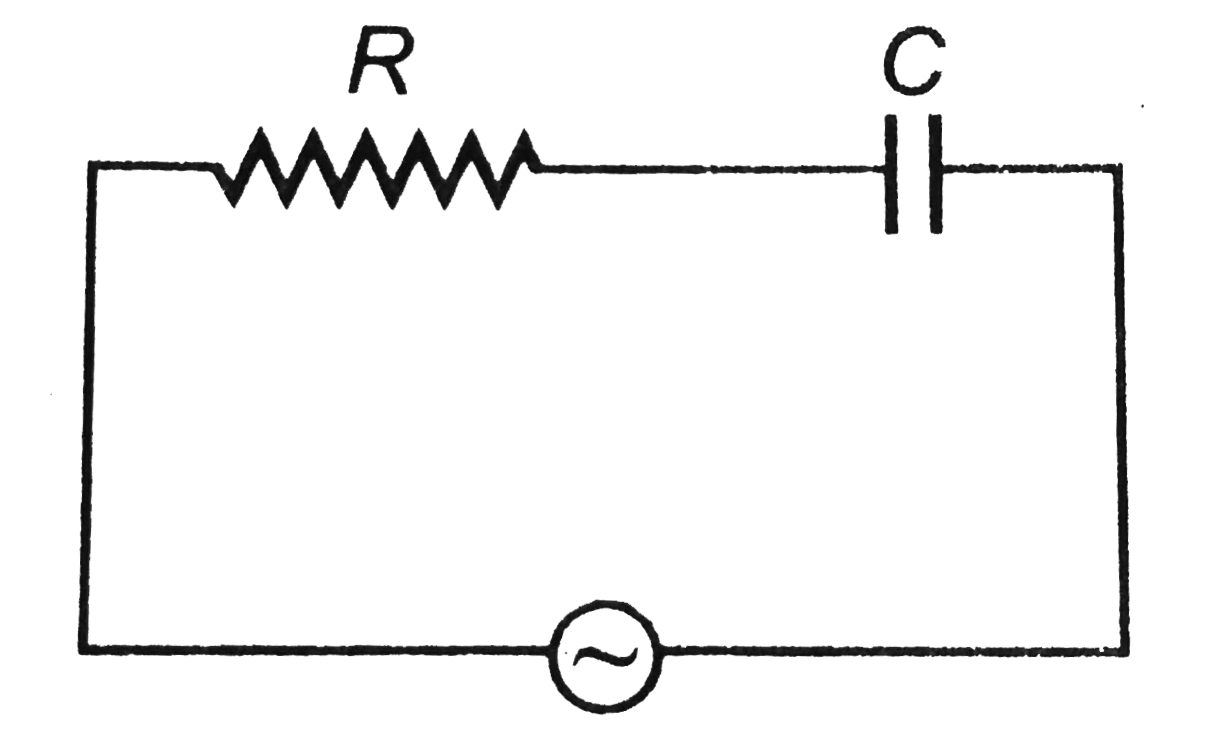
The voltage across R is 12V. The voltage across C isA8VB16VC10VDnot possible to determine unless value of R and C are given
A 31.4Ω resistor and 0.1H inductor are connected in series to a 200V, 50Hz ac source. Calculate
(ii) the voltage (rms) across the inductor and the resistor.
View SolutionAn a.c. source generating a voltage v=v+(m)sinωt is connected to a capacitor of capacitor of capacitance C. Find the expression for the current, I, flowing through it. Plot a graph of v and I versus ω t to show that the current is π/2 ahead of the voltage.
A resistor of 200Ω and a capacitor of 15.0μF are connected in series to a 220 V, 50 Hz a.c. source. Calculate the current in the circuit and the rms voltage across the resistor and the capacitor. Is the algebraic sum of these voltages more than the source voltages ? If yes, resolve the paradox.
View SolutionA resistor and an inductor are connected in series across an AC power supply . The value of current drawn from the source is 2 A . Calculate the net impedance of circuit if voltage across inductor and resistor are 100 V and 80 V respectively.
View SolutionA 10μF capacitor and a 15Ω resistor are connected in series across a 220 V 50 Hz source . Calculate the value of rms current .
View SolutionA coil of resistance R and inductance L is connected across an a.c power supply of r.m.s. voltage V. The average power dissipated in the coil is,
View Solution
