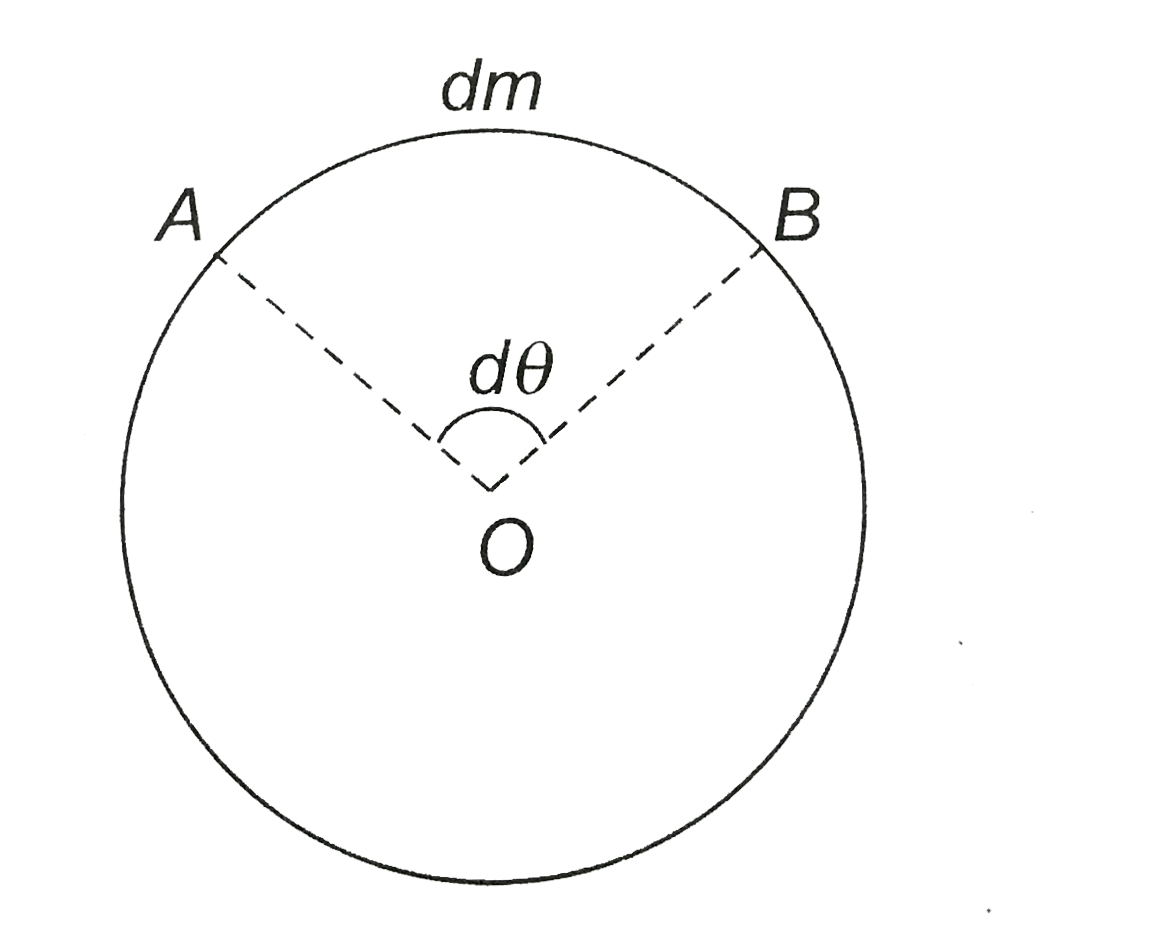
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
Consider a small length of ring that subtends an angle dθ at the center.
dm=m2πRdl=m2πRRdθ=m2πdθ
dm is moving in the circle and the necessary centripetal force is provide by component of tension.
2Tsin(dθ2)=dmω2R=mω2R2πdthη
As dθ is small
sin(dθ2)
2Tdθ2=T×dθ=mω2R2πdθ
T=mω2R2π

Topper's Solved these Questions
Similar Questions
A ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.
View Solution
Knowledge Check
A thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity ω. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
AωM(m+M)Bω(M−2M)(M+2m)CωM(M+2m)Dω(M+2m)MA thin circular ring of mass m and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass M are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity ω'=
Aω(m+2M)mBω(m−2M)(m+2M)Cωm(m+M)Dωm(m+2M)A thin circular ring of mass M and radius r is rotating about its axis with constant angular velocity ω . Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring . The ring now rotates with angular velocity given by
A(M+2m)ω2mB2MωM+2mC(M+2m)ωMDMωM+2m
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(i)Current produced due to motion of ring
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω, Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity ω=
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity omega. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be
View Solution
