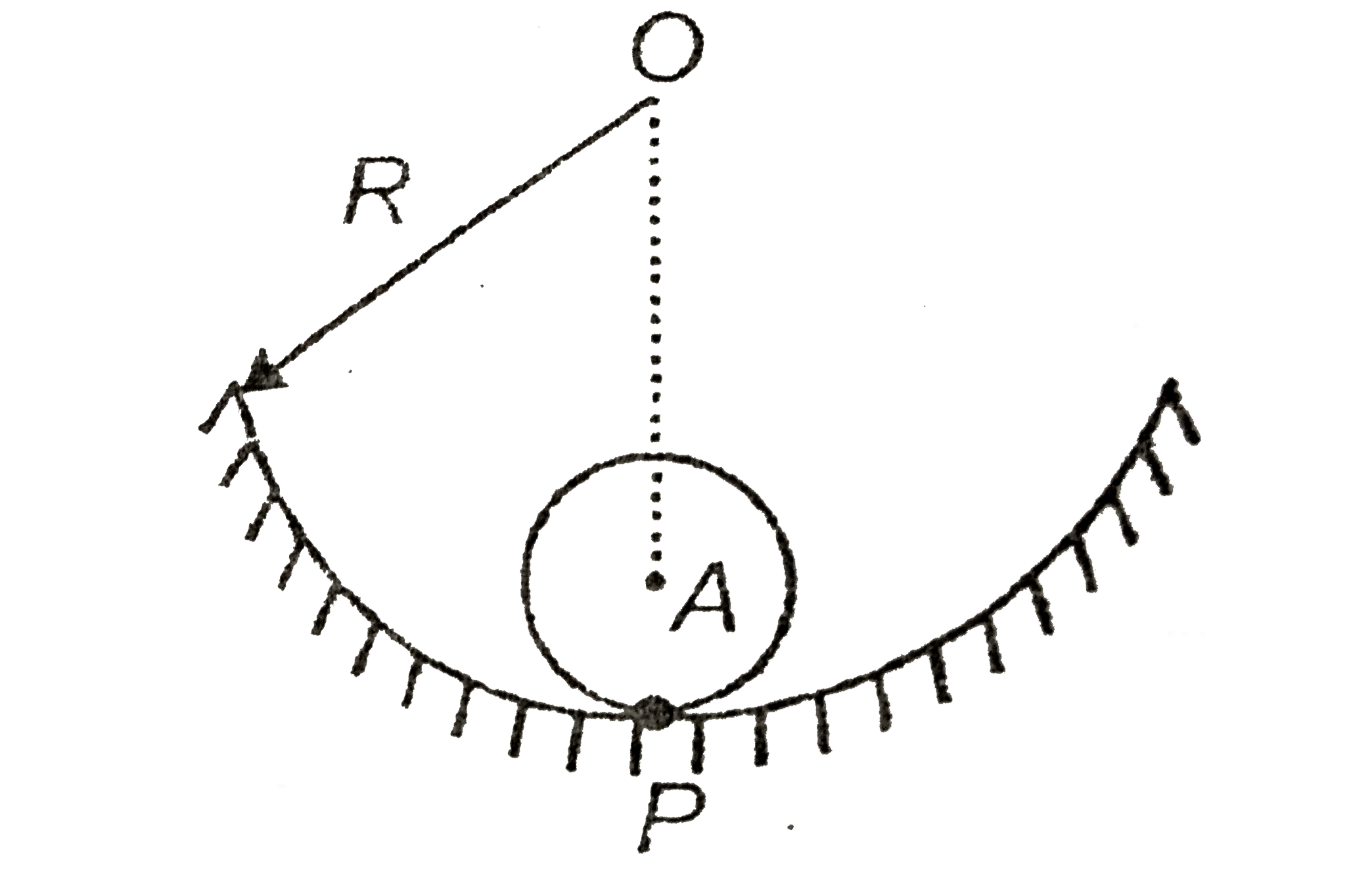
A ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.
A ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2pisqrt((n(R-r))/(3g)) then find the value of n.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:6

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for A ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2pisqrt((n(R-r))/(3g)) then find the value of n. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023
Class 11PHYSICSSIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.

    AThe kinetic energy of rotation is 15mv20.
    BThe total kinetic energy is 710mv20.
    CThe mechanical energy (assume the ground as reference) is mgR+710mv20.
    DAll options are correct.

  • A solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?

    AMR22
    BMR2
    C32MR2
    D2MR2

  • A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is

    Av/R
    BContinuously increasing
    CDependent on mass M
    DIndependent of radius (R)