A ring of radius R=4m is made of a highly dense material. Mass of the ring is m1=5.4×109kg distributed uniformly over its circumference. A highly dense particle of mass m2=6×108kg is placed on the axis of the ring at a distance x0=3m from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
The correct Answer is:A, C
To solve the problem step by step, we will calculate the displacement of the ring when the particle is at the center of the ring and then find the speed of the particle at that instant.
Given Data:
- Radius of the ring, R=4m
- Mass of the ring, m1=5.4×109kg
- Mass of the particle, m2=6×108kg
- Initial distance of the particle from the center of the ring, x0=3m
Step 1: Calculate the Displacement of the Ring
1. Assume the displacement of the ring is x.
2. The displacement of the particle when the ring moves is x0−x, where x0=3m.
3. The center of mass of the system will not move, so we can use the principle of conservation of momentum:
m1⋅x=m2⋅(x0−x)
4. Substituting the values:
5.4×109⋅x=6×108⋅(3−x)
5. Expanding the equation:
5.4×109⋅x=1.8×109−6×108⋅x
6. Rearranging the equation:
5.4×109⋅x+6×108⋅x=1.8×109
(5.4×109+0.6×109)⋅x=1.8×109
6×109⋅x=1.8×109
7. Solving for x:
x=1.8×1096×109=0.3m
Step 2: Calculate the Speed of the Particle
1. Using conservation of energy:
- Initial potential energy when the particle is at x0=3m:
Ui=−Gm1m2√R2+x20=−G⋅5.4×109⋅6×108√42+32
- Final potential energy when the particle is at the center of the ring (displacement x=0.3):
Uf=−Gm1m2√R2+(x0−x)2=−G⋅5.4×109⋅6×108√42+(3−0.3)2
2. Kinetic energy at the final state:
Kf=12m1v21+12m2v22
- Since v2=9v1 (from momentum conservation):
Kf=12m1v21+12m2(9v1)2
=12m1v21+12m2⋅81v21
=12(m1+81m2)v21
3. Setting initial potential energy equal to final kinetic energy:
Ui−Uf=Kf
- Substitute values and solve for v1.
Final Results:
1. Displacement of the ring: x=0.3m
2. Speed of the particle: Calculate v1 using the energy conservation equation.
- Radius of the ring, R=4m
- Mass of the ring, m1=5.4×109kg
- Mass of the particle, m2=6×108kg
- Initial distance of the particle from the center of the ring, x0=3m
1. Assume the displacement of the ring is x.
2. The displacement of the particle when the ring moves is x0−x, where x0=3m.
3. The center of mass of the system will not move, so we can use the principle of conservation of momentum:
m1⋅x=m2⋅(x0−x)
4. Substituting the values:
5.4×109⋅x=6×108⋅(3−x)
5. Expanding the equation:
5.4×109⋅x=1.8×109−6×108⋅x
6. Rearranging the equation:
5.4×109⋅x+6×108⋅x=1.8×109
(5.4×109+0.6×109)⋅x=1.8×109
6×109⋅x=1.8×109
7. Solving for x:
x=1.8×1096×109=0.3m
1. Using conservation of energy:
- Initial potential energy when the particle is at x0=3m:
Ui=−Gm1m2√R2+x20=−G⋅5.4×109⋅6×108√42+32
- Final potential energy when the particle is at the center of the ring (displacement x=0.3):
Uf=−Gm1m2√R2+(x0−x)2=−G⋅5.4×109⋅6×108√42+(3−0.3)2
2. Kinetic energy at the final state:
Kf=12m1v21+12m2v22
- Since v2=9v1 (from momentum conservation):
Kf=12m1v21+12m2(9v1)2
=12m1v21+12m2⋅81v21
=12(m1+81m2)v21
3. Setting initial potential energy equal to final kinetic energy:
Ui−Uf=Kf
- Substitute values and solve for v1.
1. Displacement of the ring: x=0.3m
2. Speed of the particle: Calculate v1 using the energy conservation equation.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.1
20 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
A ring of radius R=8m is made of a highly dense-material Mass of the ring is mR=2.7×109kg distributed uniformly over its circumference. A particle of mass (dense) mp=3×108kg is palced on the axis of the ring speed (in cm/sec) of the particle at the instant when it passes through centre of ring .
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of 2√3 m from the centre.
View Solution
Knowledge Check
A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
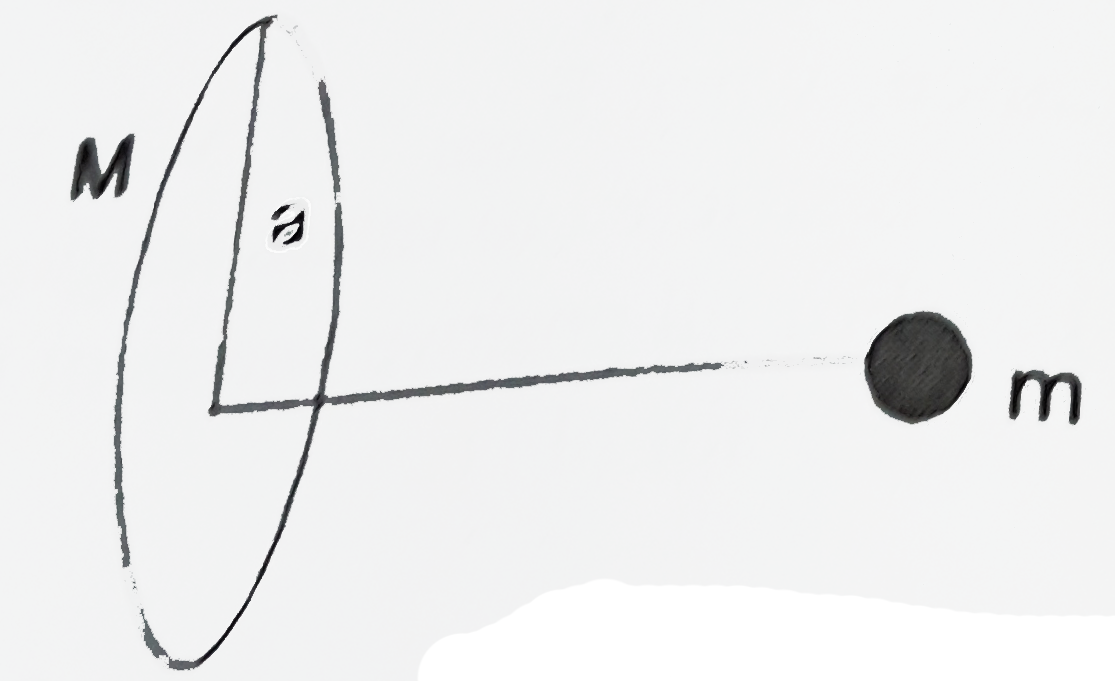
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2A particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
Gravitational potential energy of this system.A−GMm√a2+x2BGMmaCGMmxDNone of theseA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
A√GMaB√GM2a(mM)C√GM2a(Mm)D√GMa(MM+m)
A particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionMass of 10 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View SolutionA charge of 4×10−9C is distributed uniformly over the circumference of a conducting ring of radius 0.3m. Calculate the field intensity at a point on the axis of the ring at 0.4m from its centre, and also at the centre.
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View Solution