A ring whose diameter is 1 meter, oscillates simple harmonically in a vertical plane about a nail fixed at its circumference. The time period will be
1/4 sec
1/2sec
1 sec
2sec
The correct Answer is:D
To find the time period of a ring oscillating in a vertical plane about a nail fixed at its circumference, we can follow these steps:
1. Identify the Diameter and Radius of the Ring:
- Given that the diameter of the ring is 1 meter, we can calculate the radius r as:
r=Diameter2=1m2=0.5m
2. Understand the Formula for Time Period:
- The time period T for a simple pendulum is given by the formula:
T=2π√lg
- In our case, the effective length l is equal to the distance from the pivot point (the nail) to the center of the ring, which is equal to the radius of the ring.
3. Calculate the Effective Length:
- Since the pivot is at the circumference of the ring, the effective length l for our calculation is:
l=2r=2×0.5m=1m
4. Substitute Values into the Time Period Formula:
- Now substituting l and the acceleration due to gravity g≈9.8m/s2 into the time period formula:
T=2π√1m9.8m/s2
5. Calculate the Square Root:
- First, calculate the square root:
√19.8≈0.319
6. Calculate the Time Period:
- Now substitute this back into the time period formula:
T≈2π×0.319≈2×3.14×0.319≈2.006s
7. Final Result:
- Therefore, the time period of the oscillation is approximately:
T≈2s
Summary:
The time period of the ring oscillating in a vertical plane about a nail fixed at its circumference is approximately 2 seconds.
---
- Given that the diameter of the ring is 1 meter, we can calculate the radius r as:
r=Diameter2=1m2=0.5m
- The time period T for a simple pendulum is given by the formula:
T=2π√lg
- In our case, the effective length l is equal to the distance from the pivot point (the nail) to the center of the ring, which is equal to the radius of the ring.
- Since the pivot is at the circumference of the ring, the effective length l for our calculation is:
l=2r=2×0.5m=1m
- Now substituting l and the acceleration due to gravity g≈9.8m/s2 into the time period formula:
T=2π√1m9.8m/s2
- First, calculate the square root:
√19.8≈0.319
- Now substitute this back into the time period formula:
T≈2π×0.319≈2×3.14×0.319≈2.006s
- Therefore, the time period of the oscillation is approximately:
T≈2s
The time period of the ring oscillating in a vertical plane about a nail fixed at its circumference is approximately 2 seconds.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on centre of mass)
12 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular displacement, velocity and acceleration)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A uniform cirucular disc of 25cm radius oscillates in its own plane about points on its circumference. Calculate the time of oscillation (g=9.8ms−2)
View SolutionStarting from the origin a body oscillates simple harmonically with a period of 2s . After time 1x second willthe kinetic energy be 75% of its total energy , then value of x is
View Solution
Knowledge Check
A uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A2π√2RgBπ√2RgCπ2√RgDπ√R2gA uniform semi circular ring of radius R and mass m is free to oscillate about its one end in its vertical plane as shown in the figure. Find time period of SHM of its centre of mass of the ring (take π2=10)
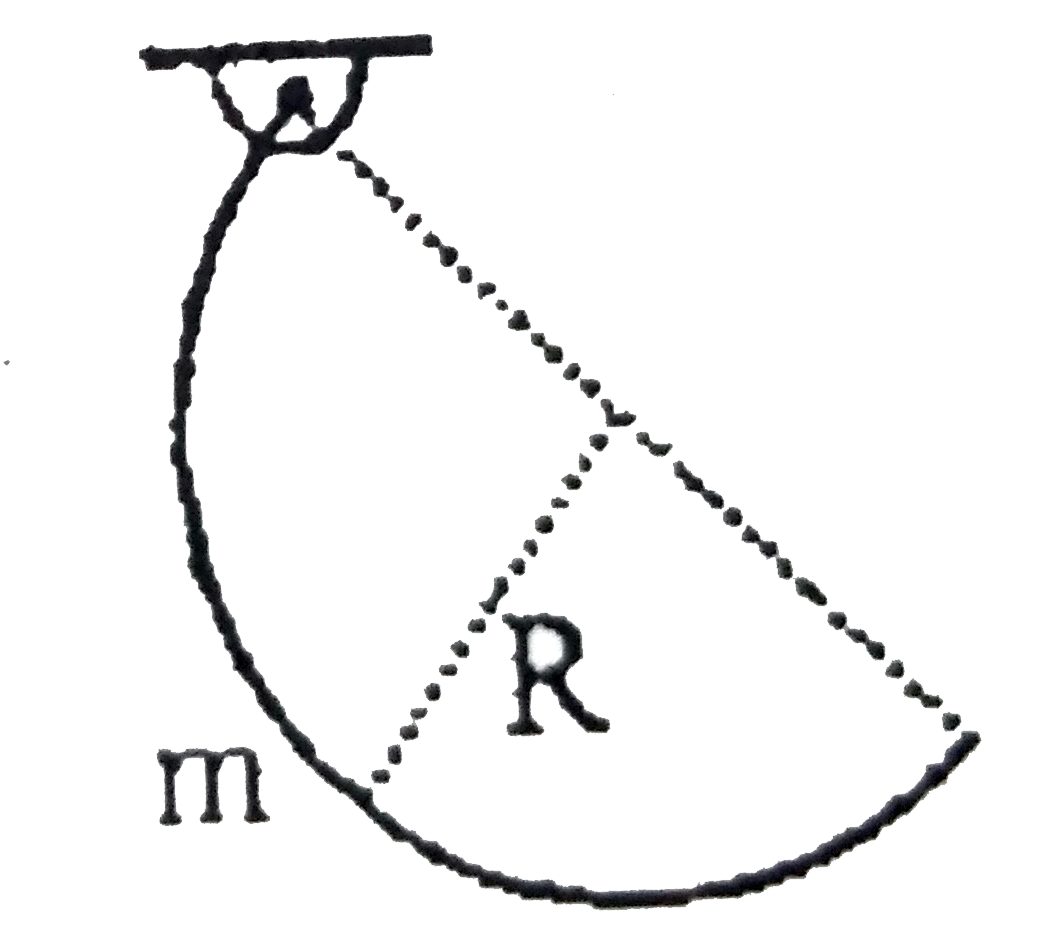 A2π√RgB2π√Rg(√207)C2π√2RgD2π√Rg(145)
A2π√RgB2π√Rg(√207)C2π√2RgD2π√Rg(145)Starting from the origin, a body oscillates simple harmonically with a period of 2 s. After what time will its kinetic energy be 25% of the total energy?
A112sB16sC14sD13s
A ring is oscillating about a horizontal axis passes through its rim. Determine time period of oscillation.
View SolutionA square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.

View SolutionA ring of radius R is suspended from its circumference and is made to oscillate about a horizontal axis in a vertical plane. The length equivalent to a simple pendulum will be :
View SolutionA disc of radius R is suspended from its circumference and made to oscillate. Its time period will be:
View SolutionThe time period of oscillations of a simple pendulum is 1 minute. If its length is increased b 44% then its new time period of oscillation will be
View Solution
