A rocket of initial mass m0 has a mass m0(1−t/3) at time t. The rocket is lauched from rest vertically upwards under gravity and expels burnt fuel at a speed u relative to the rocket vertically downward. Find the speed of rocket at t=1.
The correct Answer is:B, C
To solve the problem, we need to find the speed of the rocket at time t=1 second. We will use the principles of conservation of momentum and the given mass function of the rocket.
1. Identify the Initial Conditions:
- The initial mass of the rocket is m0.
- The mass of the rocket at time t is given by m(t)=m0(1−t3).
- The rocket is launched from rest, so the initial velocity v0=0.
2. Determine the Mass at t=1:
- Substitute t=1 into the mass function:
m(1)=m0(1−13)=m0(23)=2m03
3. Relative Speed of Fuel Expulsion:
- The speed of the expelled fuel relative to the rocket is u downward. Therefore, the speed of the expelled fuel with respect to the ground is vr=v−u, where v is the speed of the rocket.
4. Apply Conservation of Momentum:
- The momentum before and after the fuel is expelled must be equal. Initially, the momentum is m0⋅0=0.
- After expelling a small amount of fuel dm, the momentum is:
m(t)v+dm(v−u)=0
- Rearranging gives:
m(t)v=−dm(v−u)
5. Express dm:
- The change in mass dm over a small time dt can be expressed as:
dm=−m03dt
- This is derived from the mass function since the mass decreases linearly with time.
6. Substitute dm into the Momentum Equation:
- Substitute m(t) and dm:
2m03v=−(−m03)(v−u)
- Simplifying gives:
2m03v=m03(v−u)
7. Solve for v:
- Cancel m0/3 from both sides:
2v=v−u
- Rearranging gives:
v+u=0⟹v=−u
8. Calculate the Speed at t=1:
- Substitute t=1 into the expression for speed:
v=−uln(32)−g
- The final expression for the speed of the rocket at t=1 second is:
v=uln(32)−g
Final Result:
The speed of the rocket at t=1 second is:
v=uln(32)−g
- The initial mass of the rocket is m0.
- The mass of the rocket at time t is given by m(t)=m0(1−t3).
- The rocket is launched from rest, so the initial velocity v0=0.
- Substitute t=1 into the mass function:
m(1)=m0(1−13)=m0(23)=2m03
- The speed of the expelled fuel relative to the rocket is u downward. Therefore, the speed of the expelled fuel with respect to the ground is vr=v−u, where v is the speed of the rocket.
- The momentum before and after the fuel is expelled must be equal. Initially, the momentum is m0⋅0=0.
- After expelling a small amount of fuel dm, the momentum is:
m(t)v+dm(v−u)=0
- Rearranging gives:
m(t)v=−dm(v−u)
- The change in mass dm over a small time dt can be expressed as:
dm=−m03dt
- This is derived from the mass function since the mass decreases linearly with time.
- Substitute m(t) and dm:
2m03v=−(−m03)(v−u)
- Simplifying gives:
2m03v=m03(v−u)
- Cancel m0/3 from both sides:
2v=v−u
- Rearranging gives:
v+u=0⟹v=−u
- Substitute t=1 into the expression for speed:
v=−uln(32)−g
- The final expression for the speed of the rocket at t=1 second is:
v=uln(32)−g
The speed of the rocket at t=1 second is:
v=uln(32)−g
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.5
4 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.6
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.3
7 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A rocket with an initial mass of 1000kg, is launched vertically upward from rest under gravity. The rocket burns fuel at the rate of 10kg per second. The burnt matter is ejected vertically downwards with a speed of 2000m/s relative to the rocket . Find the velocity of the rocket after 1min of start.
View SolutionA rocket, with an initial mass of 1000kg, is launched vertically upwards from rest under gravity. The rocket burns fuel at the rate of 10kg per second. The burnt matter is ejected vertically downwards with a speed of 2000ms−1 relative to the rocket. If burning ceases after one minute, find the maximum velocity of the rocket. (Take g as constant at 10ms−2)
View SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
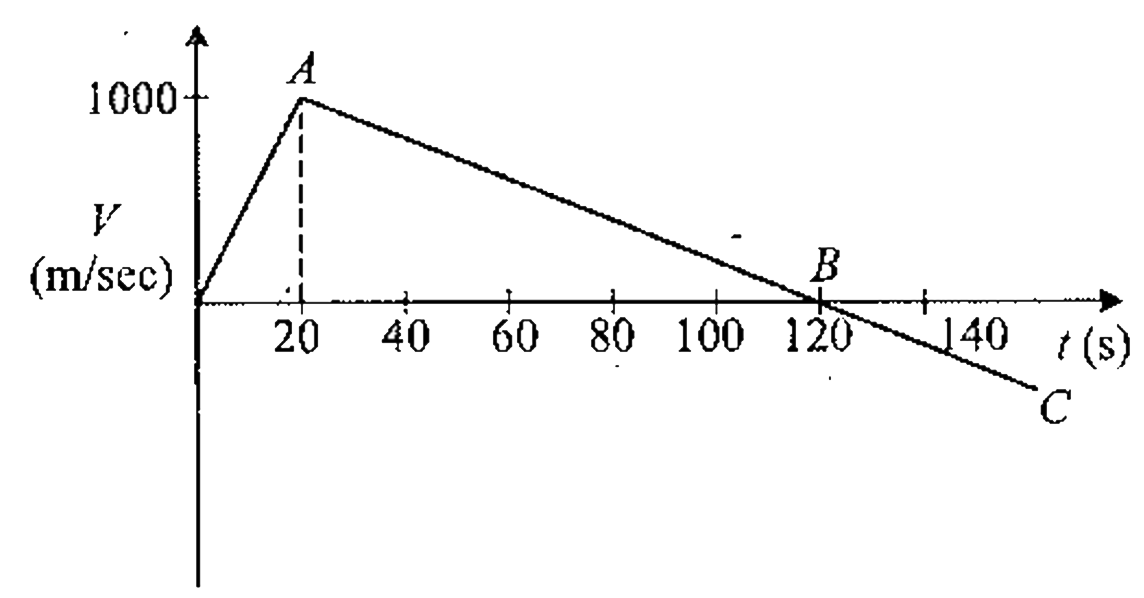
View SolutionA rocket is moving vertically upward against gravity. Its mass at time t is m=m0−μt and it expels burnt fuel at a speed u vertically downward relative to the rocket. Derive the equation of motion of the rocket but do not solve it. Here, μ is constant.
View SolutionA rocket of total mass 1000kg initially is launched from ground. The gases are ejected at the rate 20kg/s with velocity 1000 m/s relative to rocket vertically downwards. The initial acceleration of the rocket is a (in m/s2). Findag. (Take g=10m/s2)
View SolutionAt t=0, an arrow is fired vertically upwards with a speed of 100ms−1. A second arrow is fired vertically upwads with the same speed at t=5s. Then .
View SolutionA rocket fired from the earth's surface ejects 1% of its mass at a speed of 2000 ms−1 in the first second. Find the average acceleration of the rocket in the first second.
View SolutionAn object is projected vertically up from the earth’s surface with velocity √Rg where R is the radius of the earth and ‘g’ is the acceleration due to earth on the surface of earth. The maximum height reached by the object is nR. Find value of n.
View SolutionA rocket of mass m0 has attained a speed equal to its exhaust speed and that time the mass of the rocket is m. Then the ratio m0m is (neglect gravity)
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View Solution
