A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.
a. If we take rod and particle as a system, the impulse between them will be internal. We can conserve the linear momentum of rod + particle's system. Let V and ω be the velocity and angular velocity of the CM just after collision.
Using conservation of linear momentum, we have
mv0=0+Mvc..........i
Here is this case we can conserve angular momentum about any point on the rod.
And by coservation of angular momentum about the entire of mass of the rod, we get
mv0L2=lω or mv0L2=(ML212)ω...........ii
Form eqn i and ii vc=mv0M and ω=6mv0ML
We can apply conservation of anngular momentum about point of collision.
→Linitial=→Lfinal
O=I0ω(−ˆk)+Mv0l2(ˆk)
(ML2)12ω=MvcL2 .............iii
which gives ωL=6vc
Solving eqn i and iii we get the same results.
Since collisiion is completely elastic, therefore KE before collision is equa to KE after collision
or 12mv20+0=12mv2c+12ω2
or 12mv20=12M(mv0M)2+12(6mv0ML)2
Which gives mM=14 and vc=v04
Alternative method: We can apply coefficient of restitution equation at the positioinof point of collision, we have
e=(v2−v1u1−u2)
Here u1,u2,v1 and v2 are the velocities of particles and point on the rod at collision point.
u1=v0,u2=0
v1=0 and v2=vc+ωl2
As collision in elastic e=1
Substituting the values in restitution equation we get
I=(vc+ωL2)−0)v0−0⇒v0=(mv0M)+(6mv0ML)L2
Which gives mM=14
b. Velocity of point P immediately after collisionn is zero, let if be at a distance y and from CM
∴vc−ωy=0 or mv0M−(6mv0ML)y=0
which gives y=L6
∴AP=L2+L6=2L3
c. Angle rotated by the rod at time πL3v0
θ=ωt=(6mv0ML)×πL3v0=π2
The rod turns through π2 in this interval of time. the velocity of point P in y-direction will be
vy=ω=(6mv0M)×L6=v04
The resultant velocity of point P,
v=√v2c+v2y=√(v04)2+(v04)2⇒v02√2
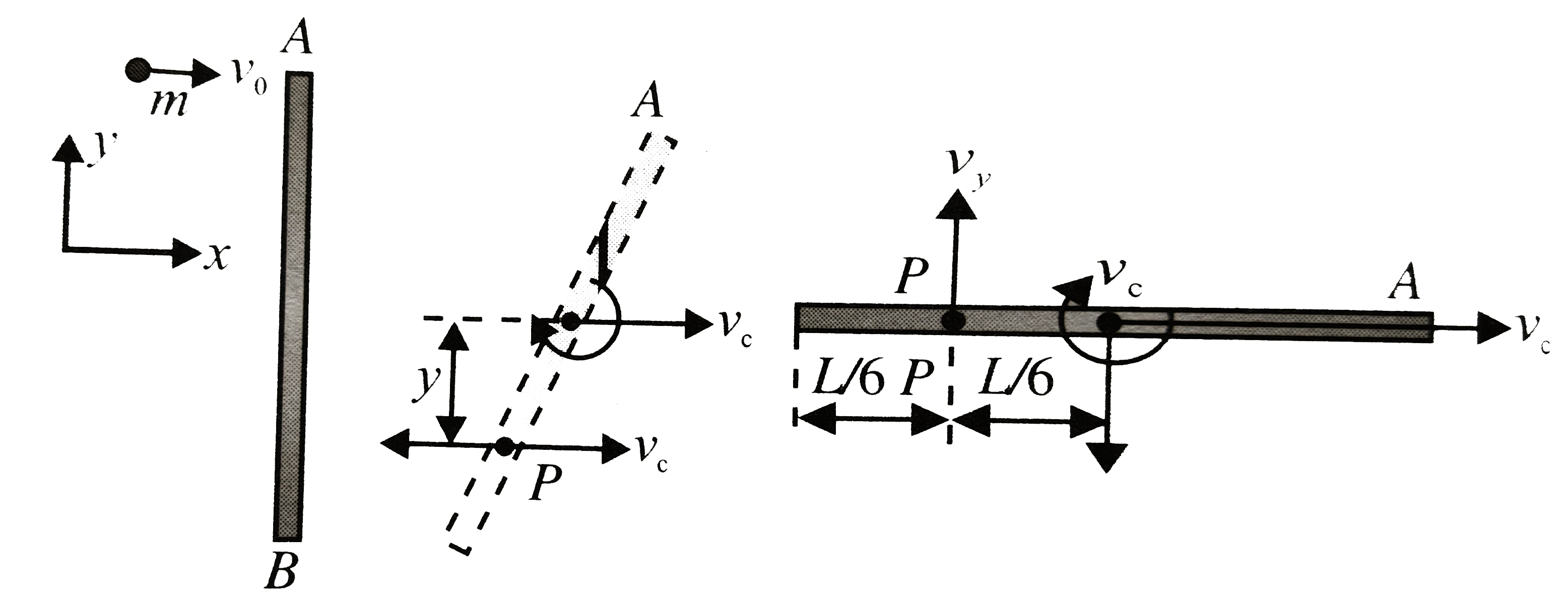
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA rod of mass M and length L is lying on a horizontal frictionless surface. A particle of mass 'm' travelling along the surface hits at one end of the rod with a velocity 'u' in a direction perpendicular to the rod. The collision is completely elastic. After collision, particle comes to rest. The ratio of masses (mM) is 1x. The value of 'x' will be_____.
View Solution
Knowledge Check
- Question 1 - Select One
A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0 - Question 2 - Select One
A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0 - Question 3 - Select One or More
A rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37∘ with the rod. The collision is elastic. After collision,
 Athe angular velocity of the rod will be 72/55v/lBthe centre of the rod will travel a distance it πl/3 in the time in which it makes half rotationCimpulse of the impact force is 24mV/55Dnone of these
Athe angular velocity of the rod will be 72/55v/lBthe centre of the rod will travel a distance it πl/3 in the time in which it makes half rotationCimpulse of the impact force is 24mV/55Dnone of these
A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
Angular velocity of rod just after collision isView SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA rod of mass m and length L is kept on a frictionless horizontal floor. A particle of same mass m moving perpendicular to the rod with a speed v strikes at the end of the rod. If coefficient of elasticity for the collision is 1 then calculate angular velocity acquired by the rod.
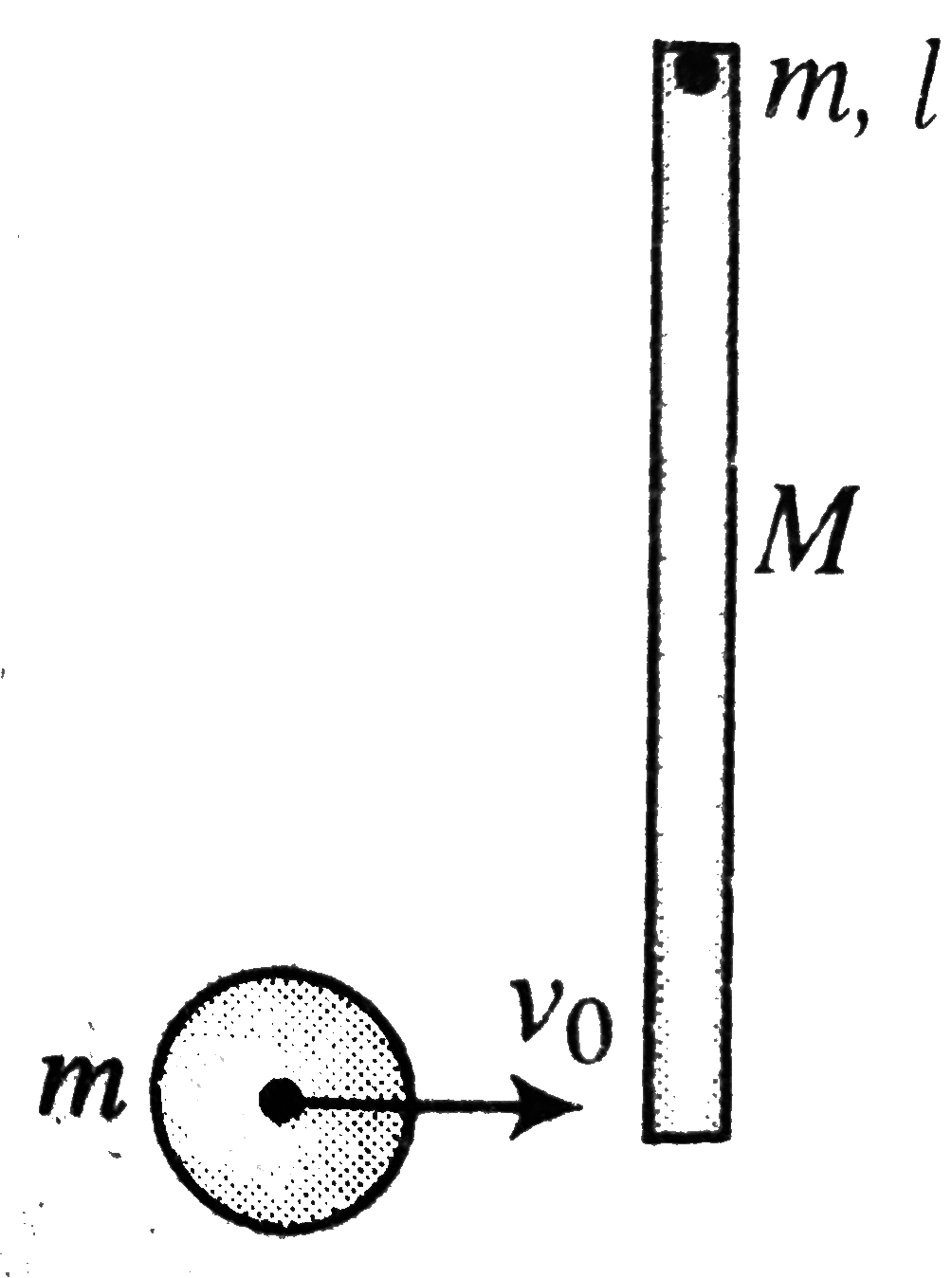
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
 View Solution
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
View Solution

