A rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
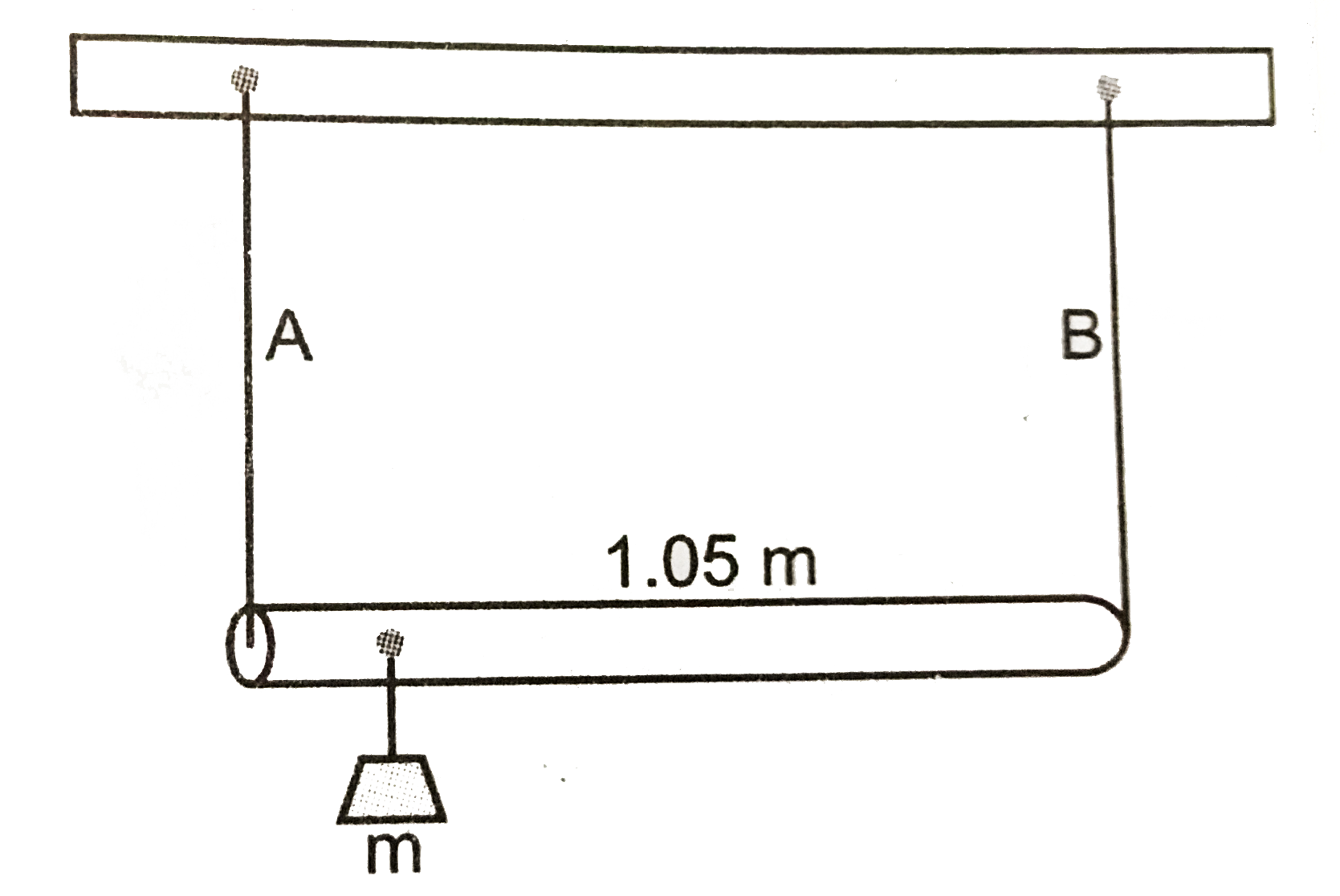
mass m should be suspended close to the wire A
mass m should be suspended close to the wire B
mass m should be suspended at the middle of the wires
mass m should be suspended from a point at a distance of 1/10 from the wire A
The correct Answer is:B
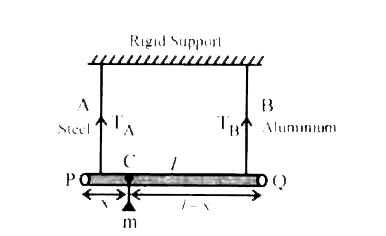
Suppose that the mass 'm' is kept at C at a distance x from the end P and let TA and TB be the tension in the wires A and B respectively. Let aA and aB be their cross sectional areas.
For the rotational equilibrium of the rod, the total torque acting on the rod should be zero.
∴TAx−TB(l−x)=0
∴TATB=l−xx ...(1)
Stress in the wire A=SA=TAaA
and stress in the wire B=SB=TBaB
To have SA=SB (equal stress)
TAaA=TBaB∴TATB=aAaB=12 ....(2)
∴l−xx=12
∴2l−2x=x∴x=2l3 and l−x=l3
Thus the mass 'm' should be suspended closer to the wire B, to have equal stresses in both the wires.
Topper's Solved these Questions
- ELASTICITYBOOK - MARVEL PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Test Your Grasp - 5
15 Videos
- CURRENT ELECTRICITYBOOK - MARVEL PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - MCQ
151 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS EXERCISE - TEST YOUR GRASP - 16
30 Videos
Similar Questions
A rod PQ of length 1.05m having negligible mass is supported at its ends by two wires one of stell (wire A), and the other of aluminium (wire B) of equal lengths as shown in fig. The cross-sectional areas of wires A and B are 1.0mm2 and 2.0mm2 respectively. At what point along the rod a load W be suspended in order to produce
(a) equal stress, (b) equal strains in both steel an aluminium.
(Ysteel=200GPa,Yaluminium=70GPa)
View SolutionA point mass m is suspended usin two wires of different material as shown in the figure. If corss-section of wire-1 and sore-2 are 3mm2and√3mm2 respectively, which of the following is correct?

View Solution
Knowledge Check
A rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
 AMass m should be suspended close to wire A to have equal stresses in both the wires.BMass m should be suspended close to B to have equal stresses in both the wires.CMass m should be suspended at the middle of the wires to have equal stresses in both the wires.DMass m should be suspended close to wire A to have equal strain on both wires.
AMass m should be suspended close to wire A to have equal stresses in both the wires.BMass m should be suspended close to B to have equal stresses in both the wires.CMass m should be suspended at the middle of the wires to have equal stresses in both the wires.DMass m should be suspended close to wire A to have equal strain on both wires.A light rod of length L is suspended from a support horizonatlly by means of two vertical wires A and B of equal lengths as show in the figure . Cross-section area of A is half that of B and Young's modulus of A is double than that
A20m/sB25m/sC22m/sD18m/sTwo wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
 AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
Alight rod of length 2 m is suspended horizontlly from the ceiling bty means of two vertical wirs of equal length tied to its ends One wire is mode of steel and is of cross - section 0.1 sq cm and the other is of brass of cross -section 0.2 sq cm Find the postion along the rod at which a wight may be hung to produce (i) equal stress in both wirs (ii) equal strain in both wires (Y for brass =10×1010Nm−2andYfor steel=20×1010Nm−2)
View SolutionA light rod of length 4.0 m is suspended from the ceiling horizontally by means of two vertical wire of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. Find out the position along the rod at which a weight may be hung to produce equal stresses in both wires.
View SolutionA wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View SolutionTwo wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

View SolutionA light rod of length L is suspended from a support horizonatlly by means of two vertical wires A and B of equal lengths as show in the figure . Cross-section area of A is half that of B and Young's modulus of A is double than that of B. A weight W is hung on the rod as shown. The value of x, so that the stress In A is same as that in B,is

View Solution
