A rod of length (f/2) is placed along the axis of a concave mirror of focal length f. If the near ead of the real image formed by the mirror just touches the far end of the rod, find its magnification.
(i) Draw a ray diagram representing the given situation.
Let AB be the object and A be the near end of the object and B be the far end of the object.
Let A'B' be the image formed.
As B' coincides with the end B at the centre of curvature,
∴ the distance of B from the mirror = 2f.
Let the length of the object be f2.
The end A is at a distance of (2f−f2).
By using 1f=1v−1u,
Determine the distance of A'B', from the mirror and find the length of the image. u= 2f - d
The magnification , m=length of the imagelength of the object
(ii) m = 2
Topper's Solved these Questions
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - Level 3
10 Videos
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - Level 1
45 Videos
- HYDROSTATICEBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICEEXERCISE - LEVEL 3 UNDERSTANDING BASED QUESTION
5 Videos
- MAGNETISMBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MAGNETISMEXERCISE - Level-3
10 Videos
Similar Questions
A thin rod of lengthf3is placed along the optic axis of a concave mirror of focal length f such that its image which is real and elongated, just touches the rod. The magnification is …..
View SolutionA rod AB of length 5 cm is placed in front of a concave mirror of focal length 10 cm as shown in figure. The length of the image of AB formed by the mirror is
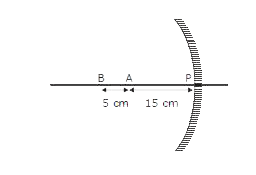
View Solution
Knowledge Check
An infinitely long rod lies along the axis of a concave mirror of focal length f. The near end of the rod is distance u>f from the mirror. Its image will have length
Aufu−fBufu+fCf2u+fDf2u−fAn infinitely long rod lies along the axis of a concave mirror of focal length f. The near end of the rod is distance u>f from the mirror. Its image will have length
Af2u+fBuf/(u−f)Cf2u−fDuf/(u+f)An infinity long rod lies along the axis of a concave mirrror of focal length f.The near end of a the rod is at a distance u>ffrom the mirror ,Its image will have a length:
Af2u−fBufu−fCf2u+fDufu+f
A thin rod of length f/3 is placed along the optic axis of a concave mirror of focal length f such that its image which is real and elongated, just touches the rod. The magnification is _____________
View SolutionA thin rod of length f/3 is placed along the optical axis of a concave mirror of focal length f such that its image whichis real and elongated just touches the rod. Calculate the magnification.
View SolutionA thin rod of length d/3 is placed along the principal axis of a concave mirror of focal length = d such that its image, which is real and elongated, just touches the rod. Find the length of the image ?
View SolutionA thin rod of length d/3is placed along the principal axis of a concave mirror of focal length =dsuch that its image,which is real and elongated,just touches the rod.Find the length of the image?
View SolutionAn object of length 6 cm is placed on the principle axis of a concave mirror of focal length f at a distance of 4 f . The length of the image will be
View Solution
