A rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
AαT21−T22l
AαT21+T22l
AαT21+T223l
AαT21−T222l
The correct Answer is:D
Heat current:
i=−kAdTdx
=−kAdT
i∫l0dx=−Aα∫T2T1TdT
il=Aα(T22−T21)2⇒i=Aα(T21−T22)2l
Topper's Solved these Questions
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Multiple Correct
Explore 25 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Comprehension
Explore 30 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Subjective
Explore 25 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICSChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionA tapering rod of length L has cross sectional radii of a and b(<a) at its two ends. Its thermal conductivity is k. The end with radius a is maintained at a higher temperature T1 and the other end is maintained at a lower temperature T2. The curved surface is insulated.
(i) At which of the two points–1 and 2– shown in the figure will the temperature gradient be higher?
(ii) Calculate the thermal resistance of the rod.
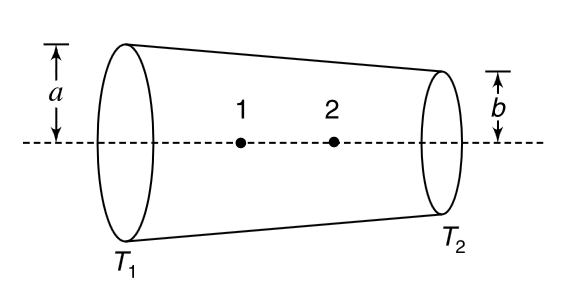
View Solution
Knowledge Check
A rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
AAα(T21−T22)lBAα(T21+T22)lCAα(T21+T22)3lDAα(T21−T22)2lA rod of length L and uniform cross-sectional area has varying thermal conductivity which changes linearly from 2K at end A to K at the other end B. The ends A and B of the rod are maintained at constant temperture 100∘C and 0∘C, respectively. At steady state, the graph of temperture : T=T(x) where x= distance from end A will be
A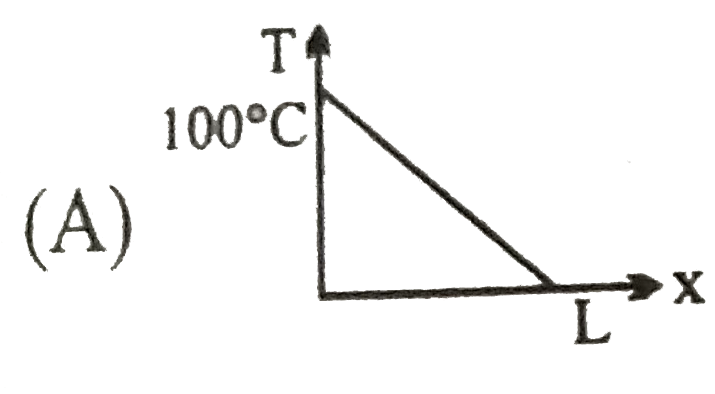 B
B C
C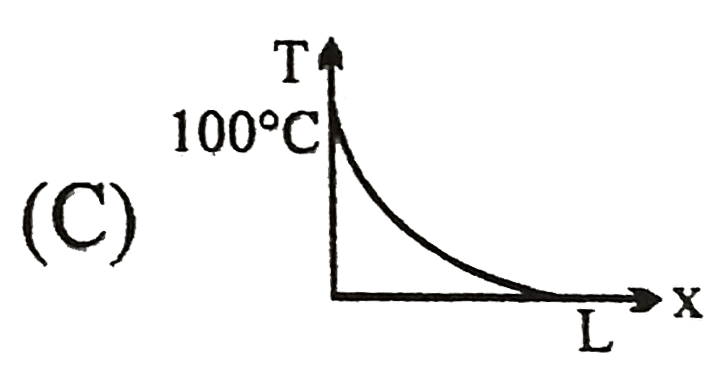 D
D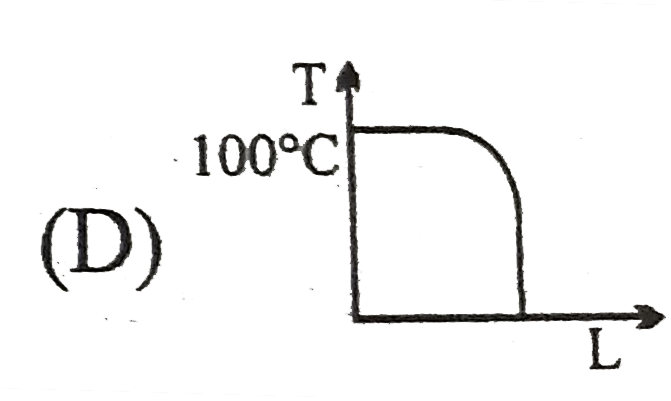
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod isA√7T0B√5T0C2T0D√3T0
A rof of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as x=α/T, where α is a constant. The ends of the rod are kept at temperatures T1 and T2. Find the function T(x), where x is the distance from the end whose temperature is T1, and the heat flow density.
View SolutionA rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k=a/T, where a is a constant. The ends of the rod are kept at temperatures T1andT2. Find the function T(x), where x is the distance from the end whose temperature is T1.
View SolutionTwo bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-ssection area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the fisrt body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View Solution
Eleven identical rods are arranged as shown in Fig. Each rod has length l, cross sectional area A and thermal conductivity of material L. Ends A and F are maintained at temperatures T1 and T2(<T1), respectively. If lateral surface of each rod is thermally insulated, the rate of heat transfer (dQdt) in each rod is
View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K1 and K2. The temperature of the free ends of the first and seconds rods are maintained at θ1 and θ2 respectively. The temperature of the common junction is
View Solution
