A rod of length L is composed of a uniform length 1/2 L of wood mass is mw and a uniform length 1/2 L of brass whose mass is mb. The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
(mw+mb)L2/12
(mw+mb)L2/6
(mw+mb)L2/3
(mw+mb)L2/2
The correct Answer is:A
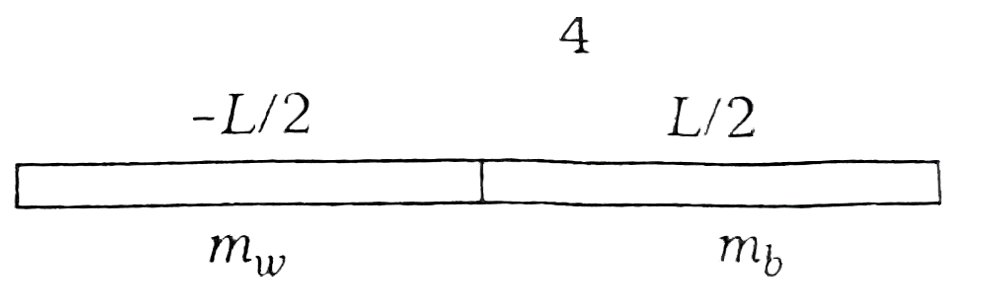
Moment of inertia,
M1=mw×(L/2)23=mw=L212
Moment of inertia,
M2=mb×(L/2)23=mb×L212
Moment of inertia,
M=M1+M2=mwL212+mb×L212=(mw+mb)L212.
Topper's Solved these Questions
Similar Questions

Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionTwo masses m1 and m2 are attached to the ends of a light rod of length l.The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is (m1=m and m2 =2m)
View Solution
Knowledge Check
A light rod of length l has two masses m1 and m2 attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
Am1m2m1+m2l2Bm1+m2m1m2l2C(m1+m2)l2D√m1m2l2A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A(m1+m2)l2B√m1m2l2Cm1m2m1+m2l2Dm1+m2m1m2l2A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A(m1+m2)l2B√m1m2l2Cm1m2m1+m2l2Dm1+m2m1m2l2
Calculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionMoment of inertia of a thin rod of mass 'M' and length 'L' perpendicular to rod at mid point is
View SolutionMoment of inertia of a thin rod of mass 'M' and length 'L' about the axis perpendicular to the rod and passing through its centre is ............
View SolutionA rod of length L is made of a uniform length L/2 of mass M1 and a uniform length L/2 of mass M2,
The M.I of rod about an axis passing through the geometrical center and ⊥ar to length
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
View Solution
