A rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance in the wire when its distance from the long wire is x.
To find the induced EMF in a rod of length l that is moving away from a long wire carrying a constant current i, we can follow these steps:
1. Identify the Magnetic Field due to the Long Wire:
The magnetic field B at a distance x from a long straight wire carrying a current i is given by:
B=μ0i2πx
where μ0 is the permeability of free space.
2. Determine the Direction of the Magnetic Field:
According to the right-hand rule, the magnetic field produced by the wire is directed into the page (or screen). We can represent this direction as −^k.
3. Identify the Velocity of the Rod:
The rod is moving away from the wire with a velocity v. We can represent this velocity vector as:
→v=v^i
where ^i is the unit vector in the direction of the x-axis.
4. Identify the Length Vector of the Rod:
The length of the rod l can be represented as:
→L=l^j
where ^j is the unit vector in the direction of the y-axis.
5. Calculate the Cross Product →v×→B:
We need to calculate the cross product of the velocity vector and the magnetic field vector:
→B=μ0i2πx(−^k)
Thus,
→v×→B=(v^i)×(μ0i2πx(−^k))
Using the right-hand rule, we find:
^i×(−^k)=^j
Therefore,
→v×→B=μ0iv2πx^j
6. Calculate the Induced EMF:
The induced EMF E is given by:
E=→L⋅(→v×→B)
Substituting the vectors:
E=(l^j)⋅(μ0iv2πx^j)
The dot product ^j⋅^j=1, thus:
E=l⋅μ0iv2πx
7. Final Result:
Therefore, the induced EMF in the rod is:
E=μ0ilv2πx
The magnetic field B at a distance x from a long straight wire carrying a current i is given by:
B=μ0i2πx
where μ0 is the permeability of free space.
According to the right-hand rule, the magnetic field produced by the wire is directed into the page (or screen). We can represent this direction as −^k.
The rod is moving away from the wire with a velocity v. We can represent this velocity vector as:
→v=v^i
where ^i is the unit vector in the direction of the x-axis.
The length of the rod l can be represented as:
→L=l^j
where ^j is the unit vector in the direction of the y-axis.
We need to calculate the cross product of the velocity vector and the magnetic field vector:
→B=μ0i2πx(−^k)
Thus,
→v×→B=(v^i)×(μ0i2πx(−^k))
Using the right-hand rule, we find:
^i×(−^k)=^j
Therefore,
→v×→B=μ0iv2πx^j
The induced EMF E is given by:
E=→L⋅(→v×→B)
Substituting the vectors:
E=(l^j)⋅(μ0iv2πx^j)
The dot product ^j⋅^j=1, thus:
E=l⋅μ0iv2πx
Therefore, the induced EMF in the rod is:
E=μ0ilv2πx
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance from the long wire is x.
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.
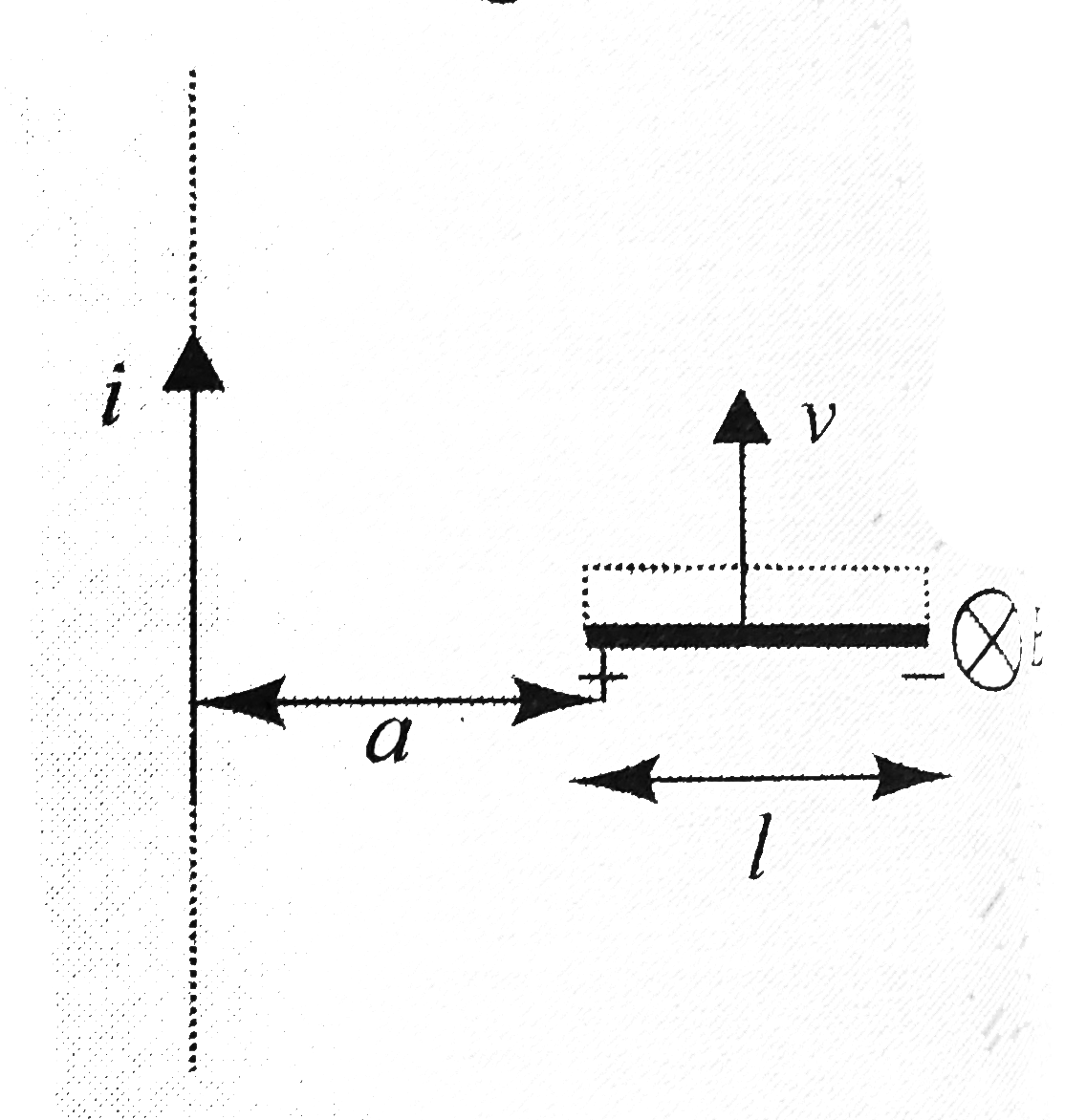
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.
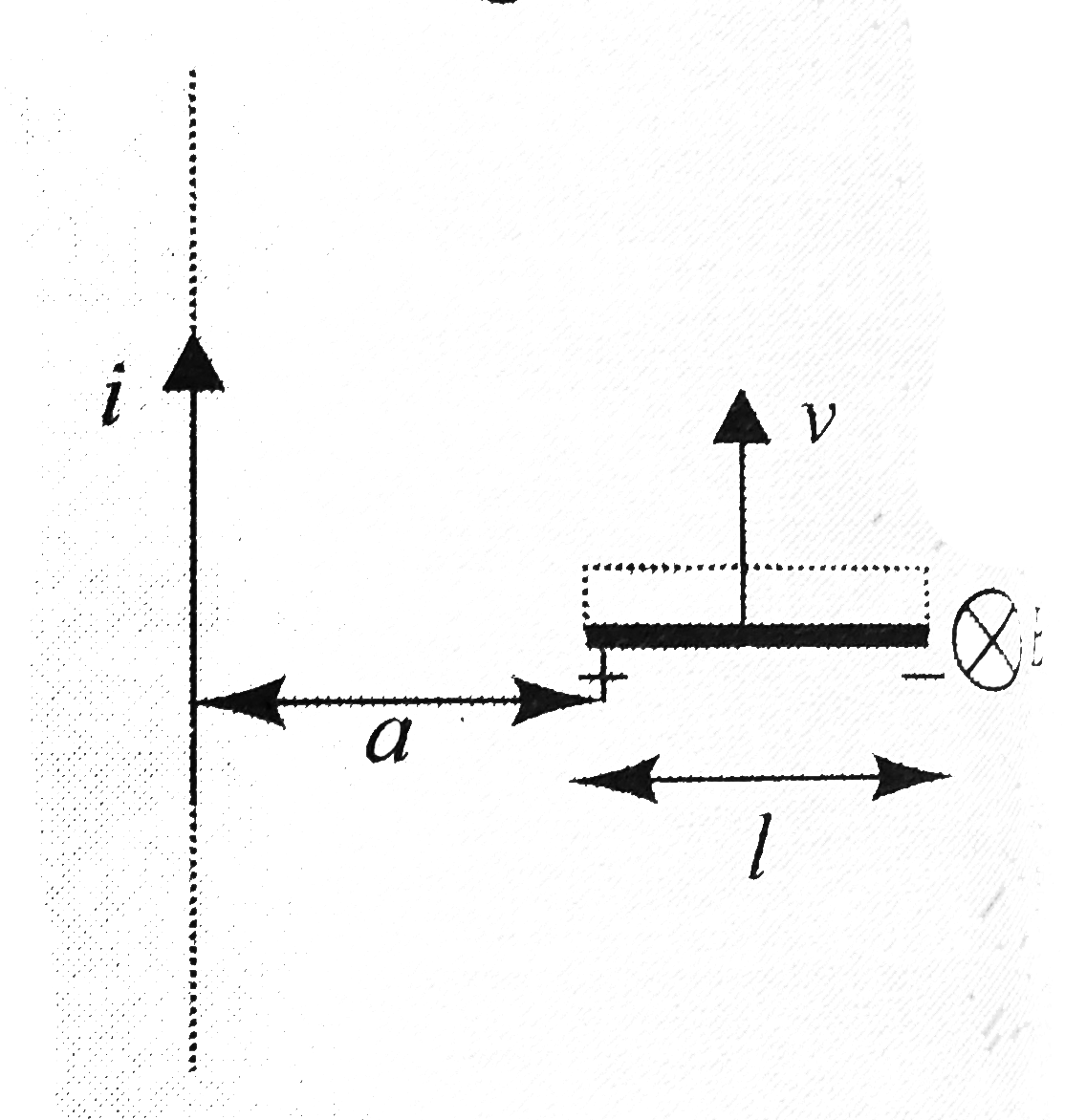
View SolutionShows an irregular shaped wire AB moving with velocity v. Find the emf induced in the wire.
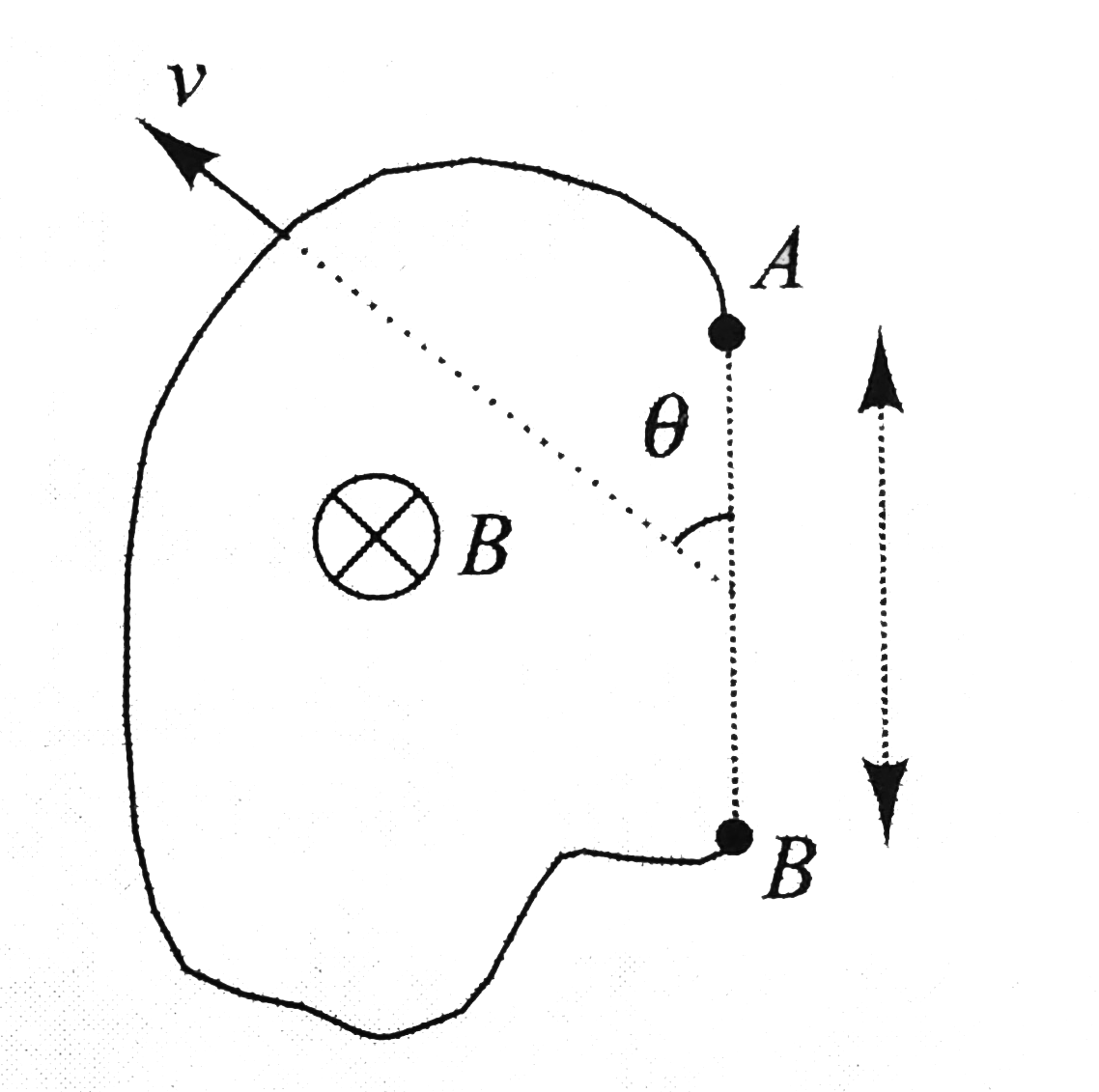
View SolutionShows an irregular shaped wire AB moving with velocity v. Find the emf induced in the wire.
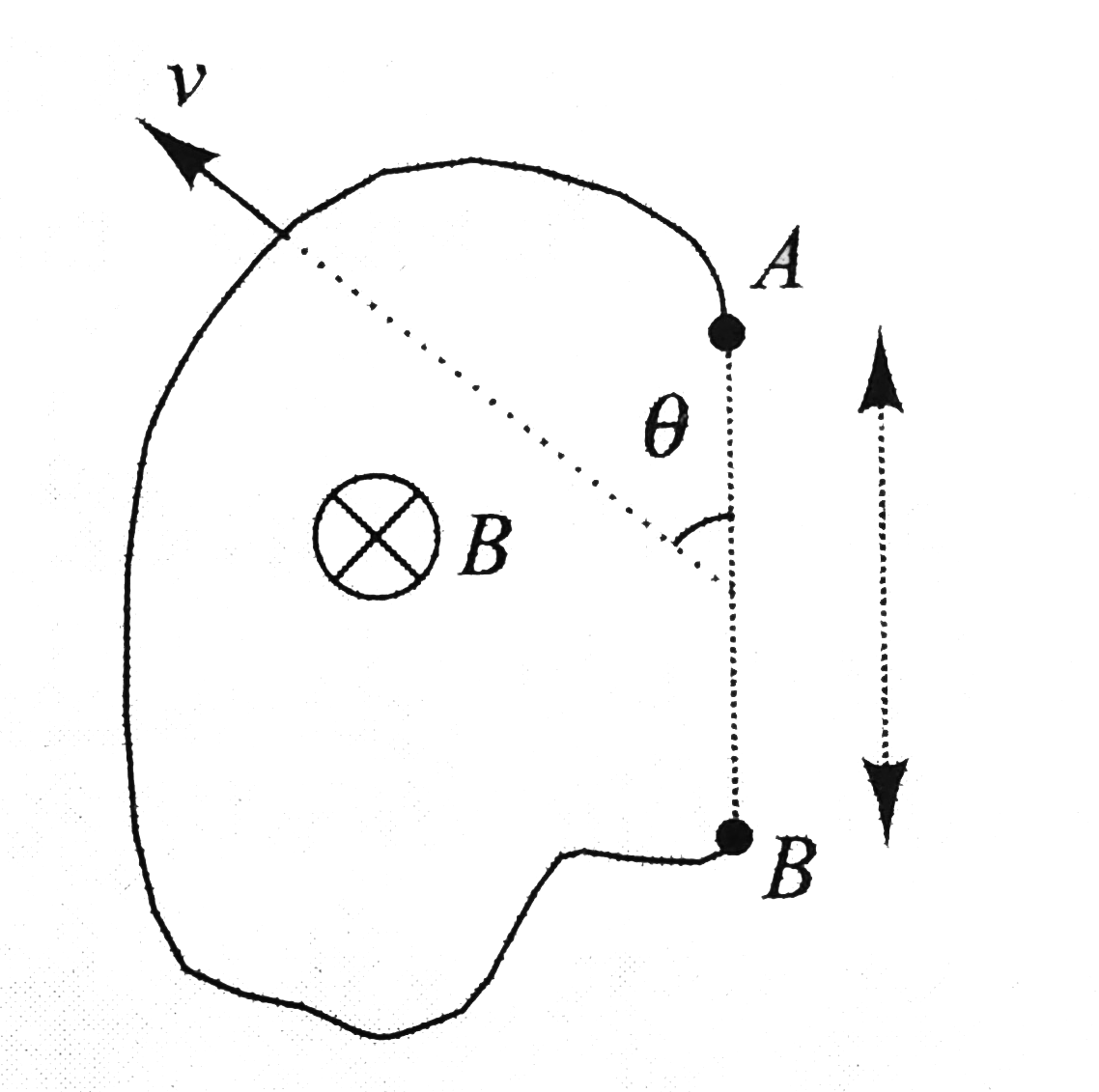
View SolutionFind →B at the origin due to the long wire carrying a current I

View SolutionA rectangular loop is moving parallel to a long wire carrying current i with a velocity v. Find the emf induced in the loop (Fig. 3.68) if its nearest end is at a distance a from the wire. Draw equivalent electrical diagram.

View SolutionA rectangular loop is moving parallel to a long wire carrying current i with a velocity v. Find the emf induced in the loop (Fig. 3.68) if its nearest end is at a distance a from the wire. Draw equivalent electrical diagram.

View SolutionFigure shows an irregular shaped wire AB moving with velocity v, as shown. Find the emf induced in the wire
View SolutionFind →B at the origin due to the long wire carrying current I.

View Solution
