A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
zero
12Blω2
Blω2
2Blω2
The correct Answer is:A
To find the potential difference between the two ends of a rotating rod in a magnetic field, we can follow these steps:
1. Understand the Setup:
- We have a rod of length L rotating about its perpendicular bisector with an angular velocity ω.
- A uniform magnetic field B exists parallel to the axis of rotation.
2. Identify Points on the Rod:
- Let the center of the rod be point O.
- The two ends of the rod are points P and Q.
- The distance from the center O to either end (i.e., OP or OQ) is L2.
3. Calculate the EMF Developed:
- The potential difference (EMF) developed between the ends of the rod can be calculated using the formula:
E=B⋅v⋅L
- Here, v is the linear velocity of the ends of the rod, which can be expressed as:
v=L2⋅ω
- Substituting v into the EMF formula gives:
E=B⋅(L2⋅ω)⋅L
- Simplifying this, we get:
E=B⋅ω⋅L22
4. Potential Difference Between Ends:
- The potential difference between the ends of the rod VP−VQ is equal to the EMF calculated:
VP−VQ=B⋅ω⋅L22
5. Final Result:
- Therefore, the potential difference between the two ends of the rod is:
VP−VQ=B⋅ω⋅L22
- We have a rod of length L rotating about its perpendicular bisector with an angular velocity ω.
- A uniform magnetic field B exists parallel to the axis of rotation.
- Let the center of the rod be point O.
- The two ends of the rod are points P and Q.
- The distance from the center O to either end (i.e., OP or OQ) is L2.
- The potential difference (EMF) developed between the ends of the rod can be calculated using the formula:
E=B⋅v⋅L
- Here, v is the linear velocity of the ends of the rod, which can be expressed as:
v=L2⋅ω
- Substituting v into the EMF formula gives:
E=B⋅(L2⋅ω)⋅L
- Simplifying this, we get:
E=B⋅ω⋅L22
- The potential difference between the ends of the rod VP−VQ is equal to the EMF calculated:
VP−VQ=B⋅ω⋅L22
- Therefore, the potential difference between the two ends of the rod is:
VP−VQ=B⋅ω⋅L22
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE98videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Worked out examples29videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
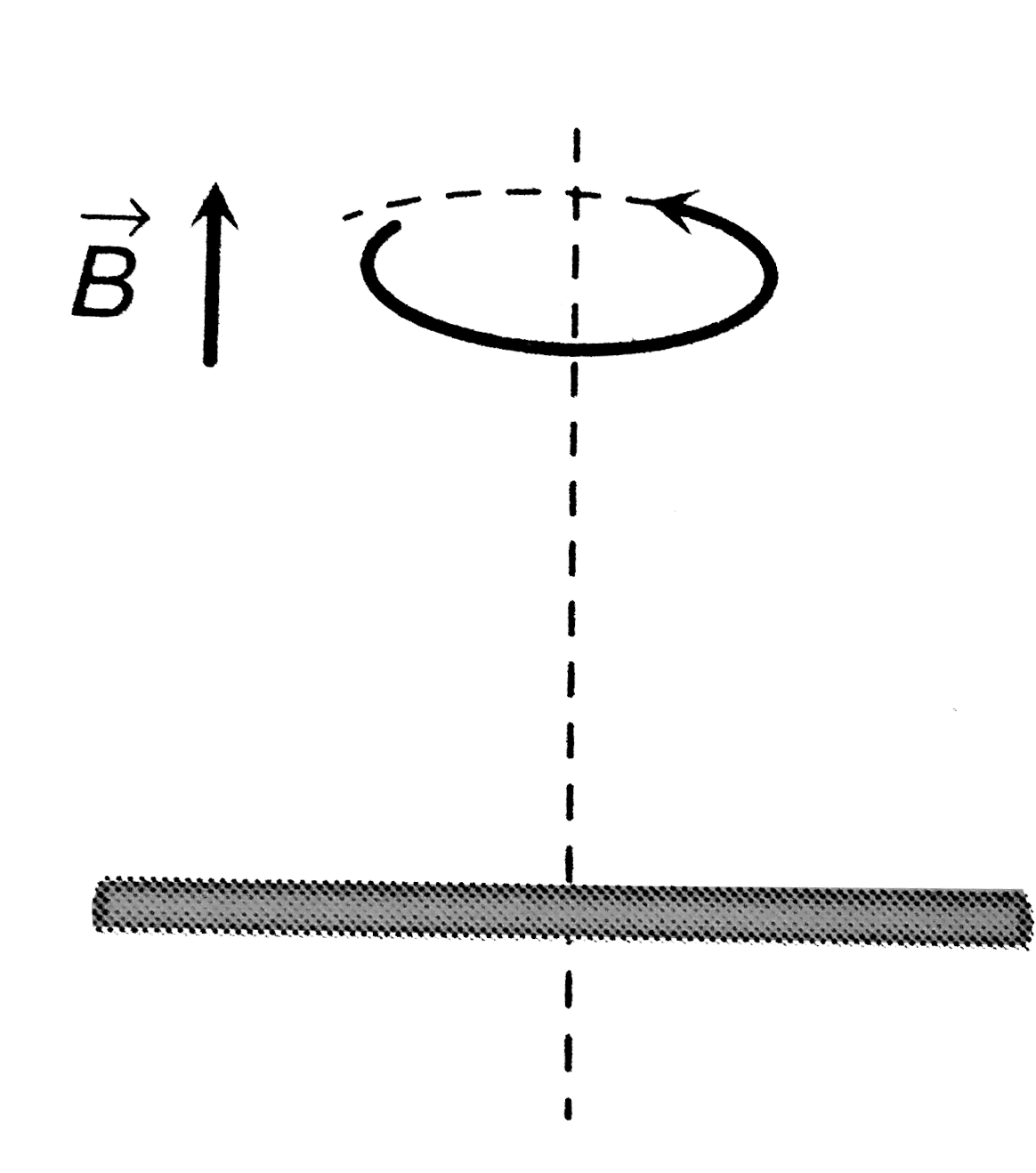 View Solution
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
 View Solution
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA metal rod length l rotates about on end with a uniform angular velocity ω. A uniform magnetic field →B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they moving in circular paths.
View SolutionA straight rod of length L is rotating about an axis passing through O and perpendicular to the plane. In the space a uniform magnetic field B exits normal to the plane of rotation. Potential difference between a & b is equal to
 View Solution
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 View Solution
View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
View SolutionA metal rod of length 15×10−2m rotates about an axis passing through one end with a uniform angular velocity of 60 rad s−1. A uniform magnetic field of 0.1 Tesla exisits in the direction of the axis of rotationn. Calculate the EMF induced between the ends of the rod.
View SolutionA metallic rod of length I rotates at angular velocity ω about an axis passing through one end and perpendicular to the rod. If mass of electron is m and its charge is -e then the magnitude of potential difference between its two ends is
View Solution

