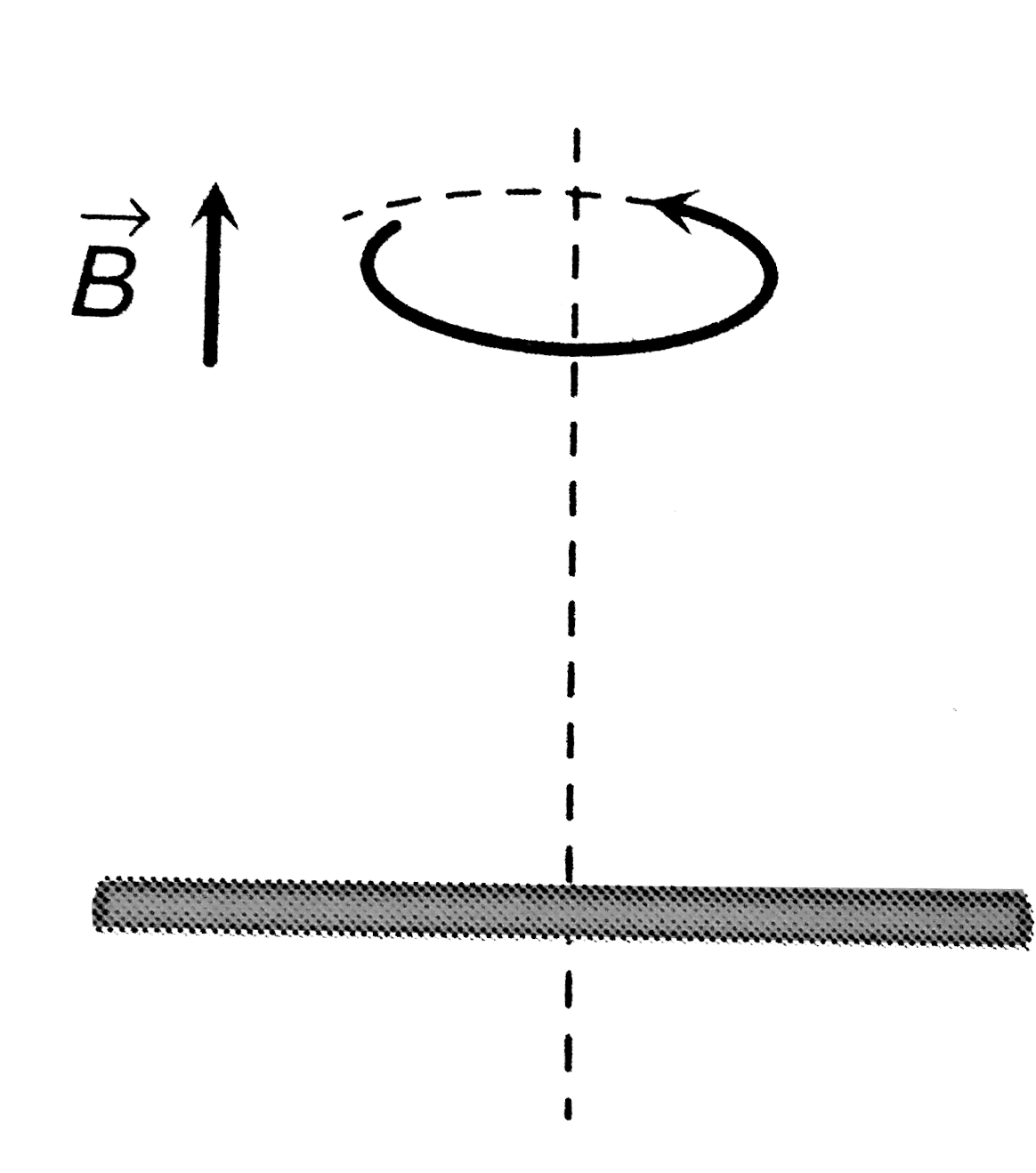
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
Bl2ω2
zero
(Bl2ω8)
2Bl2ω
The correct Answer is:B
To find the potential difference between the two ends of a rotating rod in a magnetic field, we can follow these steps:
1. Understand the Setup:
- We have a rod of length L rotating about its perpendicular bisector with an angular velocity ω.
- A uniform magnetic field B is present, parallel to the axis of rotation.
2. Define the Position:
- Let the center of the rod be at the origin. The left end of the rod is at −L2 and the right end is at +L2.
3. Consider an Element of the Rod:
- Take a small strip of the rod at a distance x from the center with a width dx.
4. Calculate the Linear Velocity:
- The linear velocity v of the strip at distance x from the center is given by:
v=ωx
5. Determine the Induced EMF (dε):
- The potential difference dϵ across the small strip can be expressed as:
dϵ=B⋅v⋅dx=B⋅(ωx)⋅dx
- This simplifies to:
dϵ=Bωxdx
6. Integrate to Find Total EMF (ε):
- To find the total potential difference ϵ between the ends of the rod, integrate dϵ from −L2 to L2:
ϵ=∫L2−L2Bωxdx
7. Perform the Integration:
- The integral can be evaluated:
ϵ=Bω∫L2−L2xdx
- The integral of x over symmetric limits is zero:
∫L2−L2xdx=0
- Therefore, we have:
ϵ=Bω⋅0=0
8. Conclusion:
- The potential difference between the two ends of the rod is:
ϵ=0
Final Answer:
The potential difference between the two ends of the rod is 0.
- We have a rod of length L rotating about its perpendicular bisector with an angular velocity ω.
- A uniform magnetic field B is present, parallel to the axis of rotation.
- Let the center of the rod be at the origin. The left end of the rod is at −L2 and the right end is at +L2.
- Take a small strip of the rod at a distance x from the center with a width dx.
- The linear velocity v of the strip at distance x from the center is given by:
v=ωx
- The potential difference dϵ across the small strip can be expressed as:
dϵ=B⋅v⋅dx=B⋅(ωx)⋅dx
- This simplifies to:
dϵ=Bωxdx
- To find the total potential difference ϵ between the ends of the rod, integrate dϵ from −L2 to L2:
ϵ=∫L2−L2Bωxdx
- The integral can be evaluated:
ϵ=Bω∫L2−L2xdx
- The integral of x over symmetric limits is zero:
∫L2−L2xdx=0
- Therefore, we have:
ϵ=Bω⋅0=0
- The potential difference between the two ends of the rod is:
ϵ=0
The potential difference between the two ends of the rod is 0.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION AND REASON
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA metal rod length l rotates about on end with a uniform angular velocity ω. A uniform magnetic field →B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they moving in circular paths.
View SolutionA straight rod of length L is rotating about an axis passing through O and perpendicular to the plane. In the space a uniform magnetic field B exits normal to the plane of rotation. Potential difference between a & b is equal to

View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
View SolutionA metal rod of length 15×10−2m rotates about an axis passing through one end with a uniform angular velocity of 60 rad s−1. A uniform magnetic field of 0.1 Tesla exisits in the direction of the axis of rotationn. Calculate the EMF induced between the ends of the rod.
View SolutionA metallic rod of length I rotates at angular velocity ω about an axis passing through one end and perpendicular to the rod. If mass of electron is m and its charge is -e then the magnitude of potential difference between its two ends is
View Solution
