A rod PQ of mass, area of cross section A, length l and young's modulus of elasticity Y is lying on a smooth table as shown in figure. A force F is applied at P. Find
(a) tension at a distance x from end P,
(b) longitudinal stress at this point,
(c) total change in length and
(d) total strain the rod.

(a)Acceleration of the rod ,a=Fm
F−Tx=(m±)a=(mlx)(Fm)
∴Tx=F(1−xl)

(b) Stress σ=FA=Tx=FA(1−xl)
(c) Change in length Δl=∫l0TxdxAY
=∫l0F(1−xl)dxAY
Δl=Fl2AY
(d) =Δll=F2AY
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - MiscellaneousExamples
4 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Exercise 15.1
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
434 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
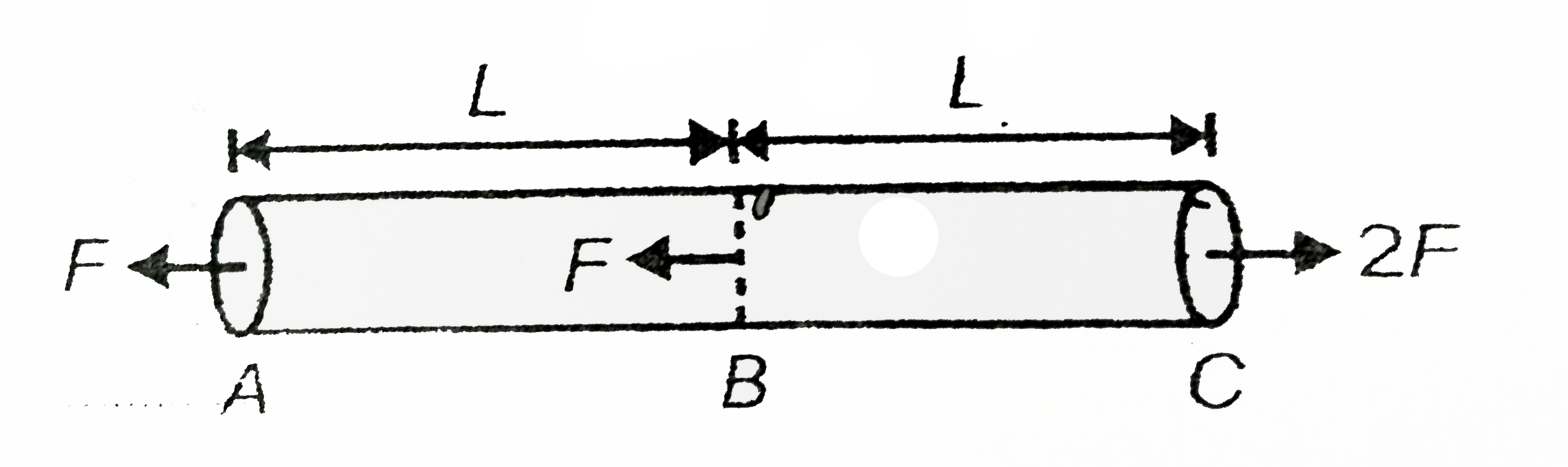
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
Select the correct alternatives.
View Solution
Knowledge Check
A string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBF should be equal to the weight of A and BCF(L-x)/LDF(L-x)MA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBFCF(L−y)LDF(l−y)MA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass (a) variea with x as:
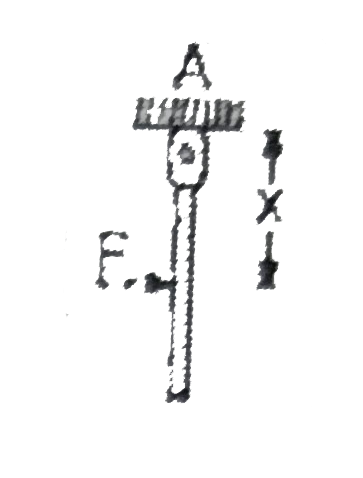 A
A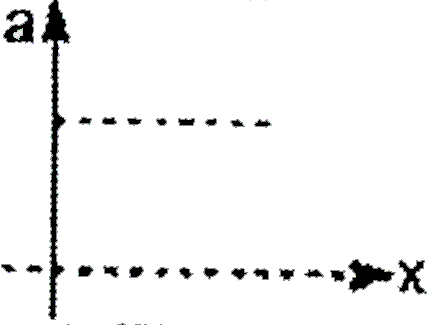 B
B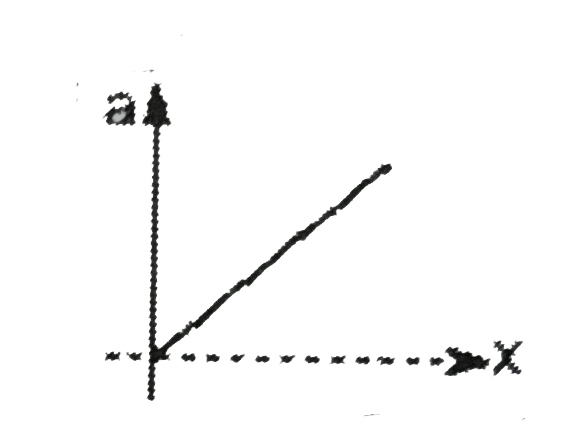 C
C D
D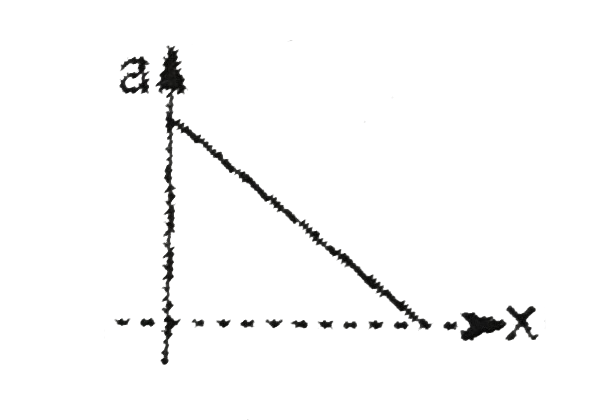
A rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
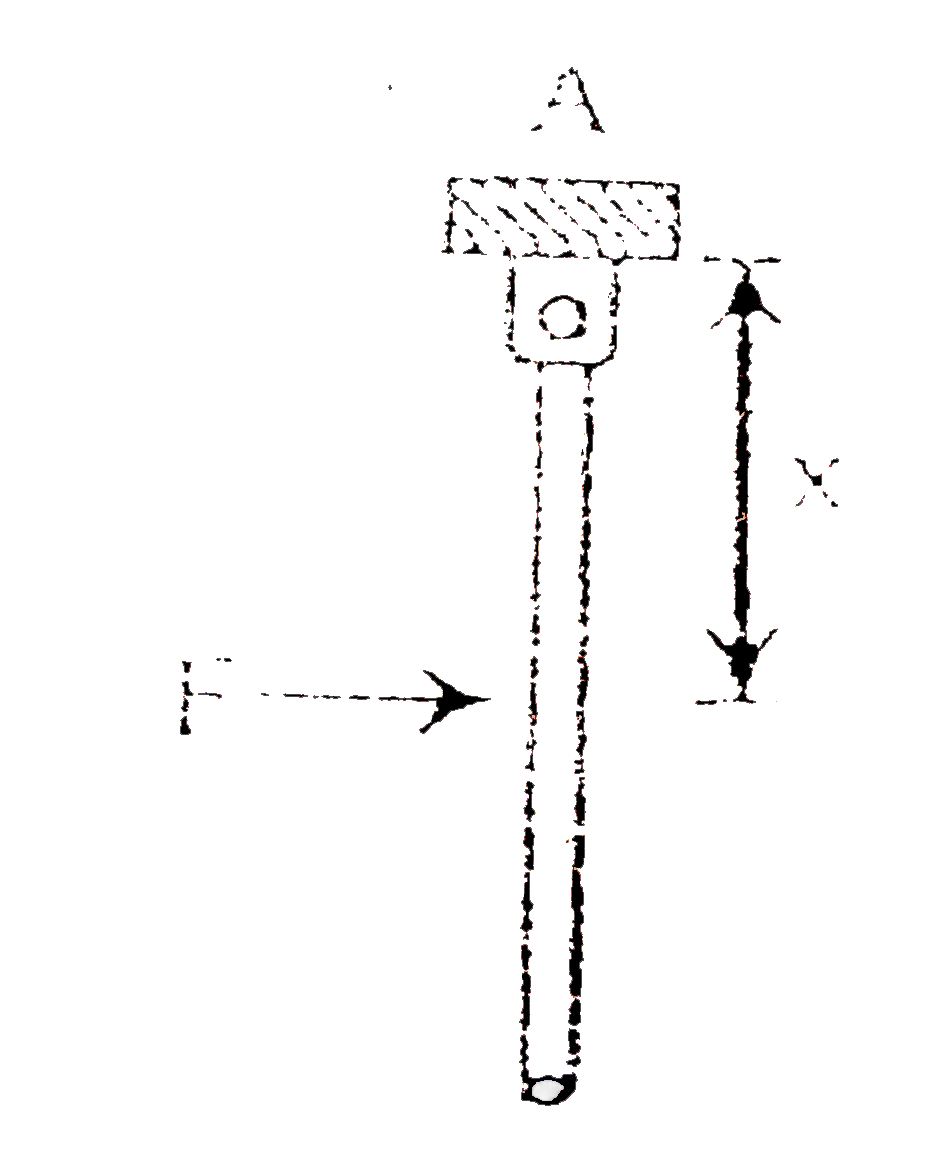
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as

View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA rod of length L and mass M is acted on by two unequal forces F1 and F2(<F)as shown in the figure.
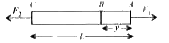
The tension in the rod at a distance y from the end A is given by
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
View Solution
