A rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
mMvr
m2Mvr
Mmvr
2Mmvr
To solve the problem of finding the velocity of the center of mass of the system consisting of a man on a ladder and a counterbalancing mass, we will follow these steps:
Step 1: Understand the System
We have a man of mass m on one end of a ladder, and a counterbalancing mass M on the other end. The man climbs the ladder with a velocity vr relative to the ladder.
Step 2: Define the Variables
- Let v0 be the velocity of the center of mass of the system.
- The mass of the ladder can be considered as M−m since it balances the mass M.
Step 3: Analyze the Motion
When the man climbs with a velocity vr relative to the ladder, both the man and the ladder will move. The man moves upward relative to the ladder, and the ladder moves downward to maintain balance with the mass M.
Step 4: Write the Momentum Conservation Equation
Initially, the system is at rest, so the total momentum is zero. As the man climbs, we can apply conservation of momentum:
m(vr−v0)+(M−m)(−v0)+Mv0=0
Where:
- m(vr−v0) is the momentum of the man.
- (M−m)(−v0) is the momentum of the ladder.
- Mv0 is the momentum of the counterbalancing mass.
Step 5: Simplify the Equation
Rearranging the momentum equation:
mvr−mv0−(M−m)v0+Mv0=0
This simplifies to:
mvr=(M−m+M)v0
mvr=(2M−m)v0
Step 6: Solve for v0
Now, we can solve for v0:
v0=mvr2M−m
Step 7: Find the Velocity of the Center of Mass
The velocity of the center of mass Vcm can be expressed as:
Vcm=m(vr−v0)+(M−m)(−v0)+Mv0M+m−m
Substituting v0 into the equation, we can find the final expression for the center of mass velocity.
Final Result
After simplification, we find that the velocity of the center of mass of the system is:
Vcm=mvr2m
Thus, the velocity of the center of mass of this system is:
mvr2m=vr2
We have a man of mass m on one end of a ladder, and a counterbalancing mass M on the other end. The man climbs the ladder with a velocity vr relative to the ladder.
- Let v0 be the velocity of the center of mass of the system.
- The mass of the ladder can be considered as M−m since it balances the mass M.
When the man climbs with a velocity vr relative to the ladder, both the man and the ladder will move. The man moves upward relative to the ladder, and the ladder moves downward to maintain balance with the mass M.
Initially, the system is at rest, so the total momentum is zero. As the man climbs, we can apply conservation of momentum:
m(vr−v0)+(M−m)(−v0)+Mv0=0
Where:
- m(vr−v0) is the momentum of the man.
- (M−m)(−v0) is the momentum of the ladder.
- Mv0 is the momentum of the counterbalancing mass.
Rearranging the momentum equation:
mvr−mv0−(M−m)v0+Mv0=0
This simplifies to:
mvr=(M−m+M)v0
mvr=(2M−m)v0
Now, we can solve for v0:
v0=mvr2M−m
The velocity of the center of mass Vcm can be expressed as:
Vcm=m(vr−v0)+(M−m)(−v0)+Mv0M+m−m
Substituting v0 into the equation, we can find the final expression for the center of mass velocity.
After simplification, we find that the velocity of the center of mass of the system is:
Vcm=mvr2m
Thus, the velocity of the center of mass of this system is:
mvr2m=vr2
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
View SolutionA stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance l with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
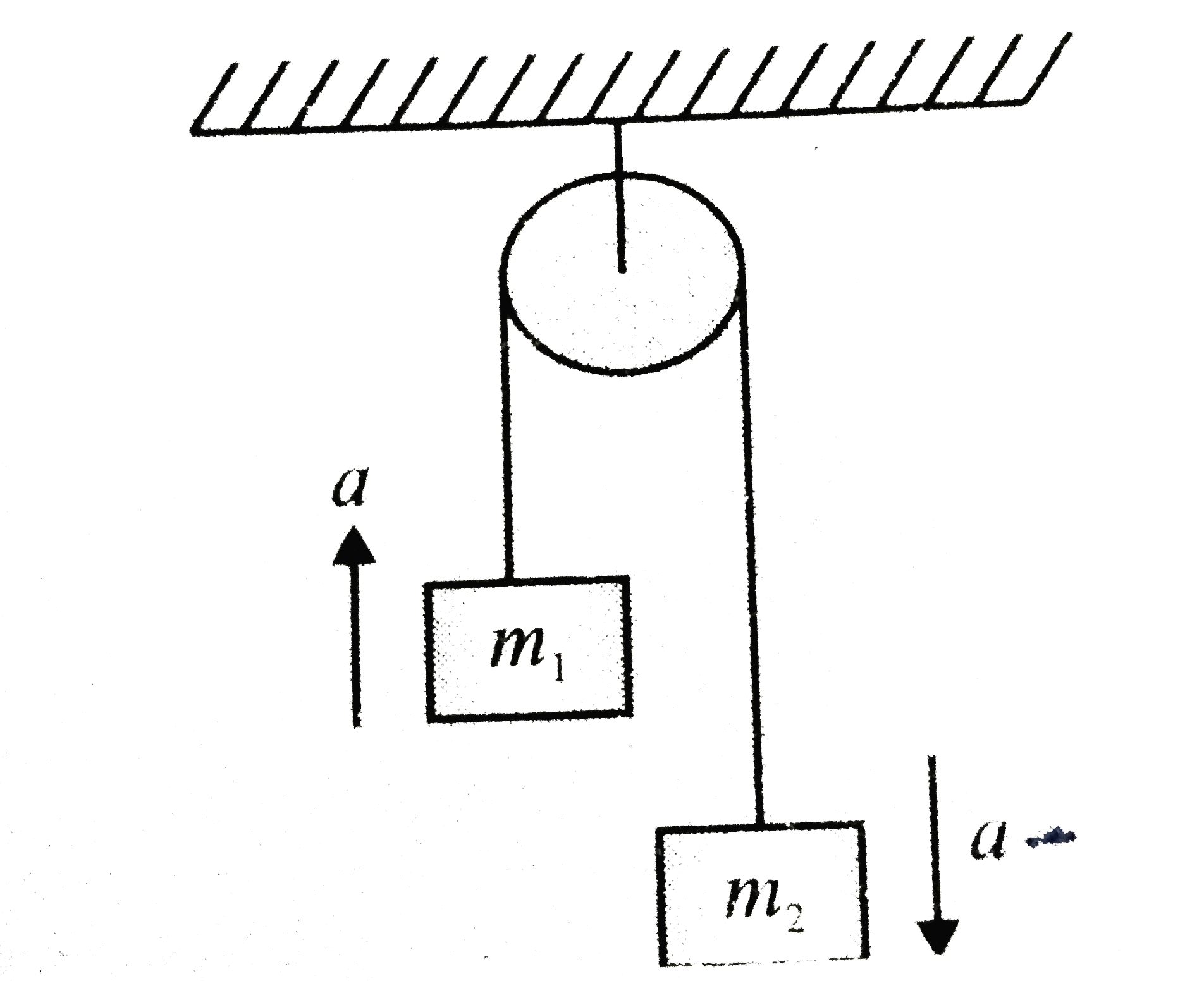
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View SolutionTwo bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
View SolutionA rope passess over a pulley which is sufficiently high. Two monkeys of equal mass climb the rope from opposite ends, one of them climbing quickly than the other relative to the rope. Assuming that the pulley and the rope are weightless and the rope is in extensible, which of monkeys will reach the top first?
View SolutionA light rope is passed over a pulley such that at its one end a block is attached , and on the other end a boy is climbing up with acceleration g2 relative to rope. Mass of the block is 30 kg and that of the boy is 40 kg. Find the tension and acceleration of the rope .
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View Solution
