A rotating disc moves in the positive direction of x-axis as shown. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment the centre C of the disc was located at origin after which
a. it moved with constant acceleration a (initial velocity zero) while the disc rotating anticlockwise with constant angular velocity ω. b. it moved with constant velocity v while the disc started rotating anticlockwise with a constant angular acceleration a (with initial angular velocity zero).

Let the coordinate of instantaneous centre of rotation at any time t be (x,y).
Now, v=ωy
√2ax=ωy
∴y2=(2aω2)x(parabola)
b. v=ωy
v=axyv
∴xy=v2α= constant (rectangular hyperbola)

Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.2
17 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.3
15 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Two heavy particles having masses m1 and m2 are situated in a plane perpendicular to line AB at a distance or r1 and r2 respectively.

a. What is the moment of inertia of the system about axis AB?
b. What is the moment of inertia of the system about an axis passing through m1 and perpendicular to the line joining m1 and m2?
c. What is the moment of inertia of the system about an axis passing through m1 and m2?
View SolutionA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?
View SolutionA uniform cylinder of radius r and mass m can rotate freely about a fixed horizontal axis. A thin cord of length l and mass m0 is would on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length x of the hanging part of the end. the wound part of the cord is supposed to have its centre of gravity on the cylinder axis is shown in figure.

View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
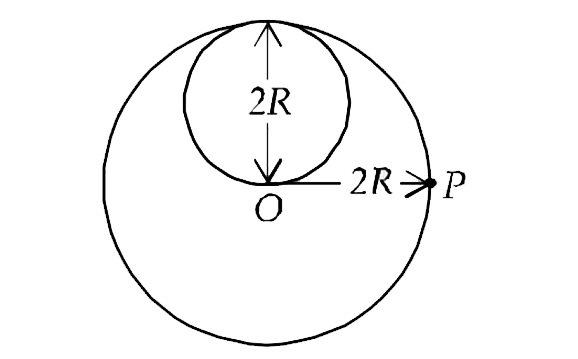
View SolutionA lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO ot the nearest integer is
View SolutionA rotating disc moves in the positive direction of the x-axis. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment of the centre c of the disc was located at the point O after which it moved with constant velocity v while the disc started rotating counterclockwise with a constant angular acceleration alhpa . the initial angular velocity is equal to zero.
View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.
View SolutionA circular disc of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular velocity ωi. Another disc of moment of inertia Ib is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed ωf. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionA horizontal disc rotates with a constant angular velocity omega=6.0rad//s about a vertical axis passing through its centre. A diameter of the disc with a velocity v^'=50cm//s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r=30cm from the rotation axis.
View SolutionA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
View SolutionA constant power is suppied to a rotating disc. The relationship between the angular velocity (ω) of the disc and number of rotations (n) made by the disc is governed by
View SolutionA non-conducting disc having unifrom positive charge Q , is rotating about its axis with unifrom angular velocity omega .The magnetic field at the centre of the disc is.
View SolutionA disc of moment of inertia la is rotating in a horizontal plane about its symmetry axis with constant angular speed co. Another discinitially at rest of moment of inertia I, is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed The loss of kinetic energy due to friction in this process is,
View SolutionA constant power is supplied to a rotating disc. The relationship between the angular velocity ( ω) of the disc and number of rotations (n) made by the disc is governed by
View SolutionA constant power is supplied to a rotating disc. The relationship of angular velocity (w) of disc anf number of rotations (n) made by the disc is governed by
View Solution
