A sensor is exposed for time t to a lamp of power P placed at a distance l. The sensor has an opening that is 4d in diameter. Assuming all energy of the lamp is given off as light, the number of photons entering the sensor if the wavelength of light is λ is
N=Pλd2thcl2
N=4λd2thcl2
N=Pλd2t4hcl2
N=Pλd2t16hcl2
The correct Answer is:A
To solve the problem of finding the number of photons entering the sensor, we can follow these steps:
Step 1: Calculate the Power per Unit Area Reaching the Sensor
The lamp emits power P uniformly in all directions. The power per unit area at a distance l from the lamp can be calculated using the formula for the surface area of a sphere:
Power per unit area=PSurface Area of Sphere=P4πl2
Step 2: Calculate the Area of the Sensor
The sensor has a diameter of 4d, so its radius r is 2d. The area A of the sensor can be calculated using the formula for the area of a circle:
A=πr2=π(2d)2=4πd2
Step 3: Calculate the Incident Power on the Sensor
The incident power Pincident on the sensor can be calculated by multiplying the power per unit area by the area of the sensor:
Pincident=(P4πl2)×(4πd2)=Pd2l2
Step 4: Calculate the Total Energy Incident on the Sensor
The total energy E incident on the sensor over a time t is given by:
E=Pincident×t=(Pd2l2)×t=Pd2tl2
Step 5: Calculate the Energy of a Single Photon
The energy Ephoton of a single photon is given by the equation:
Ephoton=hcλ
where h is Planck's constant and c is the speed of light.
Step 6: Calculate the Number of Photons
The number of photons n entering the sensor can be calculated by dividing the total energy incident on the sensor by the energy of a single photon:
n=EEphoton=Pd2tl2hcλ=Pd2tλhcl2
Thus, the final expression for the number of photons entering the sensor is:
n=Pd2tλhcl2
Final Answer:
The number of photons entering the sensor is given by:
n=Pd2tλhcl2
---
The lamp emits power P uniformly in all directions. The power per unit area at a distance l from the lamp can be calculated using the formula for the surface area of a sphere:
The sensor has a diameter of 4d, so its radius r is 2d. The area A of the sensor can be calculated using the formula for the area of a circle:
The incident power Pincident on the sensor can be calculated by multiplying the power per unit area by the area of the sensor:
The total energy E incident on the sensor over a time t is given by:
The energy Ephoton of a single photon is given by the equation:
The number of photons n entering the sensor can be calculated by dividing the total energy incident on the sensor by the energy of a single photon:
The number of photons entering the sensor is given by:
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension
44 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective
16 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
A sensor is exposed for 0.1 s to a 200 W lamp 10m away The sensor has an opening that is 20 mm in diameter. How many photons enter the sensor if the wavelength of light is 600nm? Assume that all the energy of the lamp is given off as light.
View SolutionA 200 W sodium street lamp emits yellow light of wavelength 0.6 μm. Assuming it to be 25% efficient in converting electrical energy to light, the number of photons of yellow light it emits per second is
View SolutionA modern 200 W sodium street lamp emits yellow light of wavelength 0.6 μm. Assuming it to be 25% efficient in converting electrical energy to light, the number of photons of yellow light it emits per second is
View SolutionA modern 200 W sodium street lamp emits yellow light of wavelength 0.6 μm. Assuming it to be 25% efficient in converting electrical energy to light, the number of photons of yellow light it emits per second is
View SolutionA point source is emitting 0.2 W of ultravio- let radiation at a wavelength of λ=2537Å. This source is placed at a distance of 1.0m from the cathode of a photoelectric cell. The cathode is made of potassium (Work function =2.22eV) and has a surface area of 4cm2.
(a) According to classical theory, what time of exposure to the radiation shall be required for a potassium atom to accumulate sufficient energy to eject a photoelectron. Assume that radius of each potassium atom is 2 Å and it absorbs all energy incident on it.
(b) Photon flux is defined as number of light photons reaching the cathode in unit time. Calculate the photon flux.
(c) Photo efficiency is defined as probability of a photon being successful in knocking out an electron from the metal surface. Calculate the saturation photocurrent in the cell assuming a photo efficiency of 0.1.
(d) Find the cut – off potential difference for the cell.
View SolutionA point source of monochromatic light of 1.0mW is placed at a distance of 5.0m from a metal surface. Light falls perpendicularly on the surface. Assume wave theory of light to hold and also that all the light falling on the circular area with radius =1.0×10−9m(which is few times the diameter of an atom) is absorbed by a single electron on the surface. Calculate the time required by the electron to receive sufficient energy to come out of the metal if the work function of the metal is 2.0eV.
View Solutionin an experimental set up to study the photoelectric effect a point soure fo light of power 3.2×10−3 W was taken. The source can emit monoenergetic photons of energy 5eV and is located at a distance of 0.8 m from the centre of a stationary metallic sphere of work-function 3.0 eV. The radius of the sphere is r=8..10−3 m. The efficiency of photoelectric emission is one for every 106 incident photons. Based on the information given above answer the questions given below. (Assume that the sphere is isolated and photoelectrons are instantly swepts away after the emission).
de-Broglie wavelength of the fastest moving photoelectron is
View SolutionA mercury arc lamp provides 0.10 W of UV radiation at a wavelength of λ=2537Å(all other wavelenghts having been absorbed by filters). The cathode of photoelectric device (a photo-tube) consists of potassium and has an effective area of 4cm2. The anode is located at a distance of 1 m from radiation source. The work function for potassium is ϕ0=2.22eV.
(a) According to classical theory, the radiation from the arc spreads out uniformly in space as spherical wave. What time of exposure to the radiation should be required for a potassium atoms(radius 2 Å) in the anode to accumulate sufficient energy to eject a photo-electron?
(b) What is the energy of a single photon from the source?
(C) What is the flux of photons(number per second) at the cathode? To what saturation current does this flux correspond if the photo-conversion efficiency is 5% (i.e. if each photon has a probability of 0.05 of ejecting an electron).
(d) what is the cutt off potential V0?
View Solution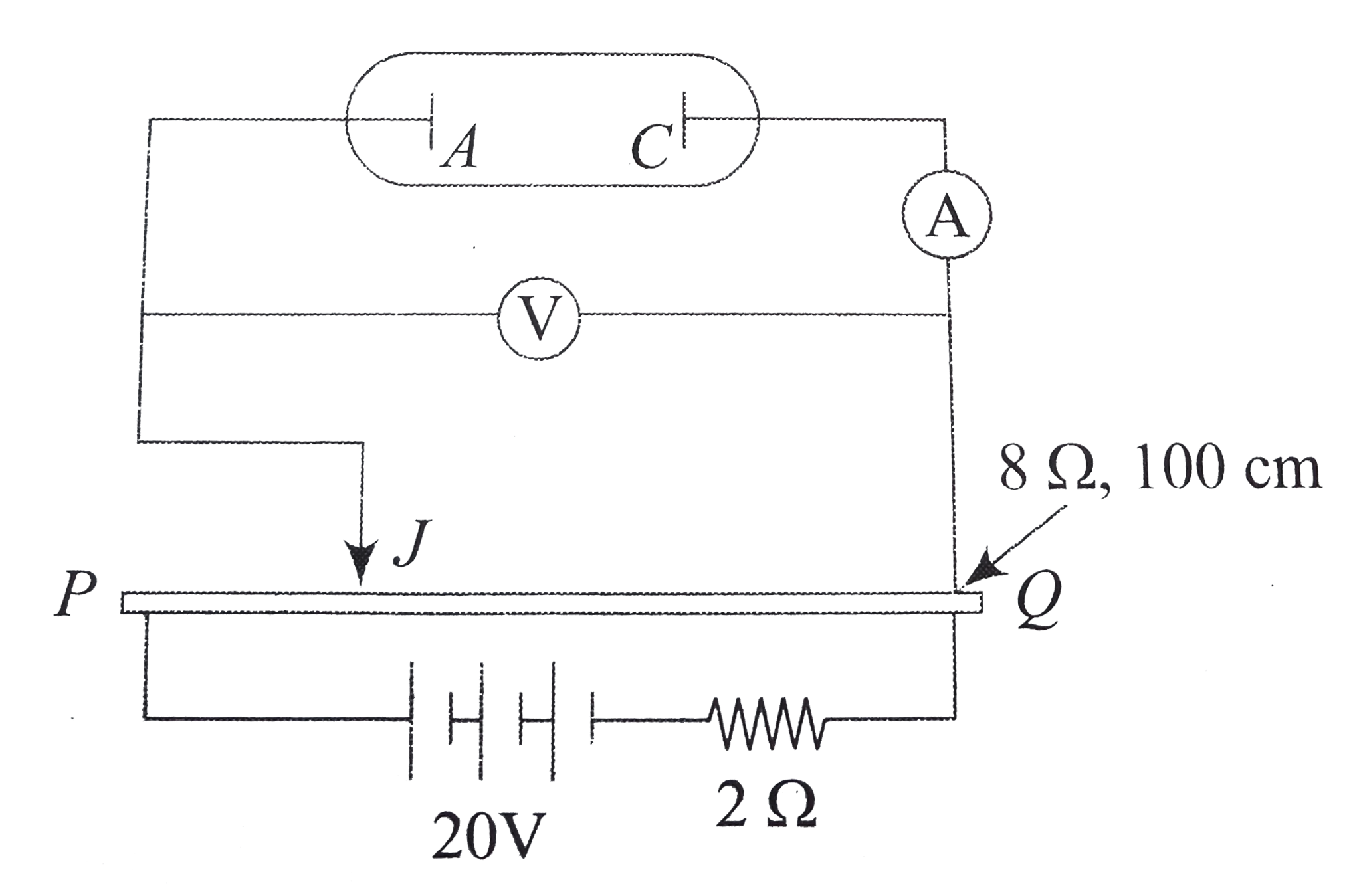
An experimental setup of verification of photoelectric effect is shown if Fig. The voltage across the electrodes is measured with the help of an ideal voltmeter, and which can be varied by moving jockey J on the potentiometer with wire. The battery used in potentiometer circuit is of 20 V and its internal resistance is 2Ω. The resistance of 100 cm long potentiometer wire is 8Ω.
The photocurrent is measured with the help of an ideal ammeter. Two plates of potassium oxide of area 50cm2 at separation 0.5mm are used in the vacuum tube. Photocurrent in the circuit is very small, so we can treat the potentiometer circuit as an independent circuit. The wavelength of various colors is as follows:
Q. It is found that ammeter current remains unchanged (2μA) even when the jockey is moved from the end P to the middle point of the potentiometer wire. Assuming that all the incident photons eject electrons and the power of the light incident is 4×10−6 W. Then, the color of the incident light is
View SolutionCalculate the number of photons emitted per second by a 10 W sodium vapour lamp. Assume that 60% of the consumed energy is converted into light. Wavelengths of sodium light =590nm.
View Solution
