A series circuit consisting of an inductance − free resistance R=0.16kΩ and coil with active resistance is connected to the mains with effective voltabe V=220V. Find the heat power generated in the coil if the effective voltage values across the resistance R and the coil are equal to V1=80V and V2=180V respectively.
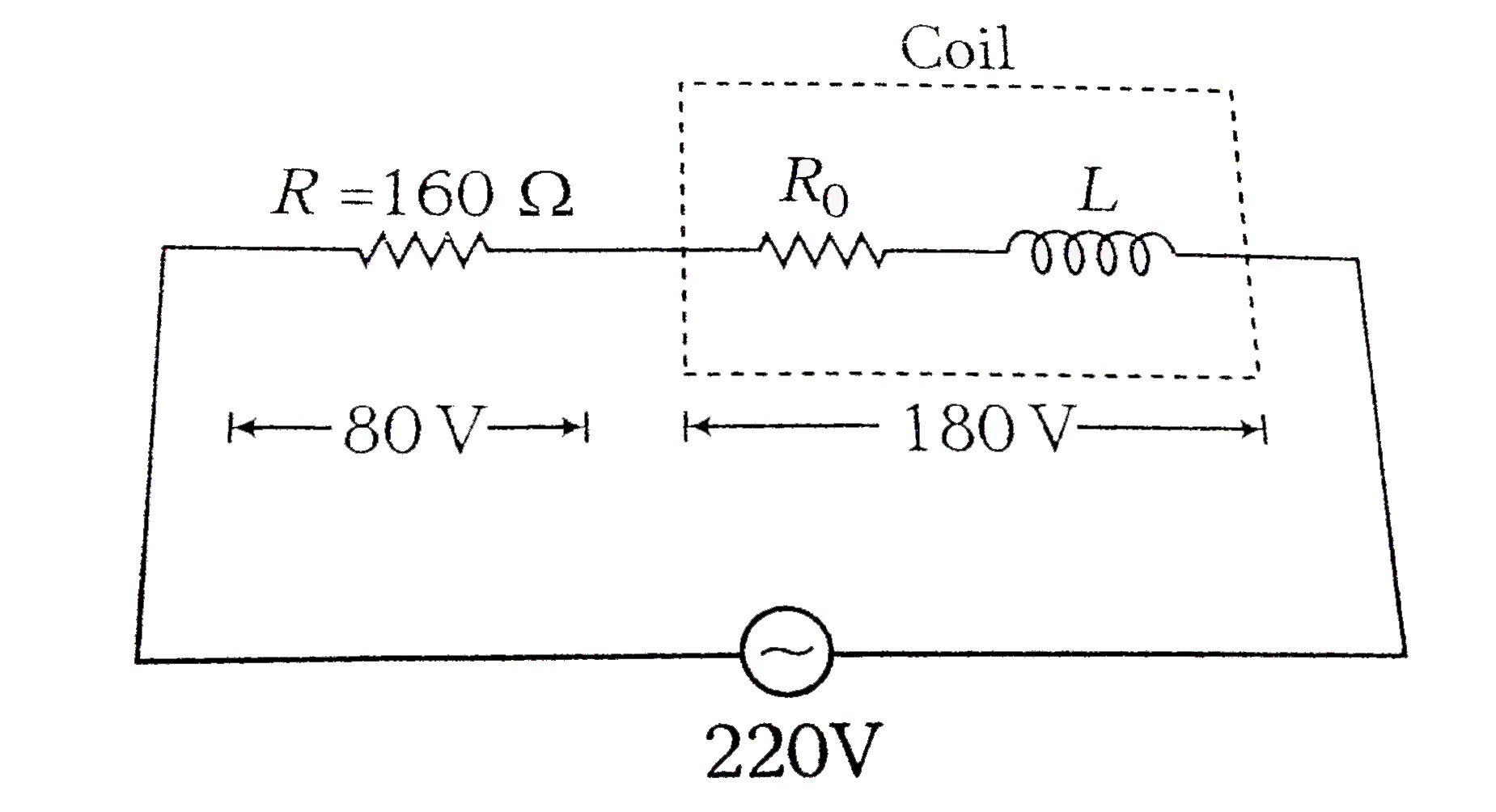
Current in the circuit,
Vr=IrmsR
⇒80=Irms×160⇒Irms=12A
Now, VR0=IrmsRR0=R02
and VL=IrmsR0=R02
⇒(VR+V2R0+V2L=(220)2
⇒(80+R02)2+XL22=(220)2
Also, V2R0+V2L=(180)2
⇒R0(2)2+(XL2)2=(180)2
Subtracting Eqs. (i) and (ii), we get
80+R02)2−(R02)2=(220)2−(180)2
⇒(80+R0)(80)=(400)(40)
Power consumed in coil,
P=I2rmsR0=(12)2×120=30W
Similar Questions
A series circuit consisting of an inductance free resistance R=0.16kΩ and a coil with active resistance is connected to the mains effective voltage V=220V Find the heat power generated in the coil if the effective voltage values across the resistance R an the coil equal to V1=80V and V_(2) =180V respectively .
View SolutionA coil with inductive resistance XL=30Ω and impedance Z=50Ω is connected to the mains with effective oltage value V=100V. Find the phase difference between the current and the voltage, as well as the heat power generated in the coil.
View Solution
Knowledge Check
- Question 1 - Select One
A 100 V voltmeter of internal resistance 20 kω is in series with a high resistance R, is connected to 110 V line . The voltmeter reads 5 V, then the value of R is
A210kΩB315kΩC420kΩD4440kΩ - Question 2 - Select One
A 100 V voltmeter of internal resistance 20kΩ n series with a high resistance R is connected to 110 V line. The voltmeter reads 5V, the value of R is -
A210kΩB315kΩC420kΩD4440kΩ - Question 3 - Select One
A 100V voltmeter of internal resistance 20kΩ in series with a high resistance R is connected to a 110V line. The voltmeter reads 5V, the value of R is
A210ΩB315ΩC420ΩD400Ω
A coil with inductive reactance XL=30Ω and impedance Z=50Ω is connected to the mains with effective voltage value V=100V Find the phase difference between the current and voltage as well as the heat power generated in the coil .
View SolutionA coil with active resistance R and inductance L was connected at the moment t=0 to a source of voltage V=Vmcosωt. Find the current in the coil as a function of time t.
View SolutionA coil and an inductance − free resistance R=25Ω are connected in parallel to the ac1 mains. Find the heat power generated in the coil provided a current I=0.90A is drawn from the mains. The coil and the resistance R carry currents I1=0.50A and I2=0.60A respectively.
View SolutionA circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
View SolutionA coil of negligible resistance is connected inseries with 90Ω resistor acorss a 120 V -60 Hz line. A voltmeter reads 36 V across the resistance. Find voltage across the coil and inductance of the coil.
View Solution

