A set of 'n' identical resistors, each of resistance 'R' when connected in series have an effective resistance 'X'. When they are connected in parallel, their effective becomes 'Y'. Find out the product of X and Y.
To solve the problem, we need to find the effective resistance when 'n' identical resistors, each of resistance 'R', are connected in series and in parallel, and then calculate the product of these two effective resistances.
1. Effective Resistance in Series (X):
- When 'n' identical resistors are connected in series, the total or effective resistance X is the sum of the individual resistances.
- Formula:
X=R+R+R+…+R(n times)=nR
- Thus, we have:
X=nR
2. Effective Resistance in Parallel (Y):
- When the same 'n' resistors are connected in parallel, the effective resistance Y can be calculated using the formula for resistors in parallel.
- Formula:
1Y=1R+1R+…+1R(n times)=nR
- Therefore, we can rearrange this to find Y:
Y=Rn
3. Product of X and Y:
- Now, we need to find the product XY:
XY=(nR)(Rn)
- Simplifying this expression:
XY=nR2n=R2
4. Final Result:
- The product of the effective resistances X and Y is:
XY=R2
Summary:
The product of the effective resistance when 'n' identical resistors are connected in series and parallel is R2.
- When 'n' identical resistors are connected in series, the total or effective resistance X is the sum of the individual resistances.
- Formula:
X=R+R+R+…+R(n times)=nR
- Thus, we have:
X=nR
- When the same 'n' resistors are connected in parallel, the effective resistance Y can be calculated using the formula for resistors in parallel.
- Formula:
1Y=1R+1R+…+1R(n times)=nR
- Therefore, we can rearrange this to find Y:
Y=Rn
- Now, we need to find the product XY:
XY=(nR)(Rn)
- Simplifying this expression:
XY=nR2n=R2
- The product of the effective resistances X and Y is:
XY=R2
The product of the effective resistance when 'n' identical resistors are connected in series and parallel is R2.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (LONG ANSWER QUESTIONS)
10 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (NUMERICAL PROBLEMS)
24 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (FILL IN THE BLANKS)
10 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A set of n identical resistors, each of resistance RΩ, when connected in series have an effective resistance XΩ and when the resistors are connected in parallel, their effective resistance is YΩ. Find the relation between R, X and Y.
View SolutionThirteen resistors each of resistance R are connected in the circuit as shown . The effective resistance between A and B is
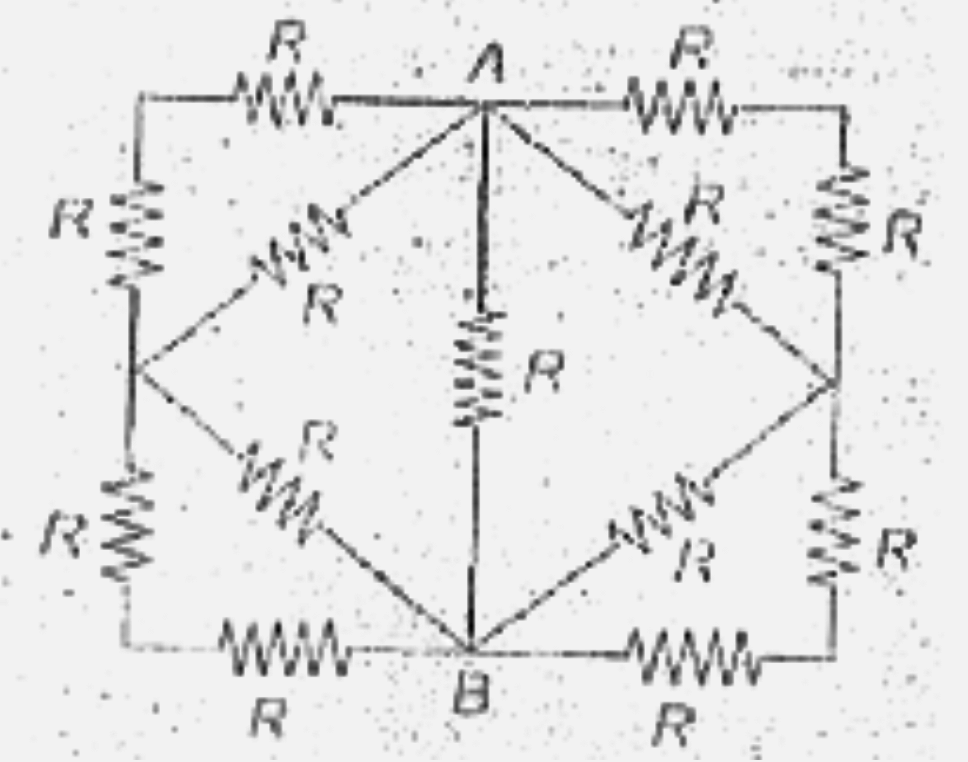
View Solution
Knowledge Check
If Four resistors each of 1Ω are connected in parallel the effective resistances will be
A0.5ΩB0.25ΩC4ΩD2Ωn resistors, each of resistances R are first connected in series so as to give an effective resistance Rs Subsequently these resistors are connected in parallel so as to give an effective resistance Rp. Then the ratio RsRp will be
An:1Bn2:1C1:n2D1:nTwo identical capacitors when joined in series have an effective capacitance of 3μF. When connected in parallel, the effective capacitance becomes 12μF. What is the capacitance of each capacitor ?
A6μFB3μFC12μFD9μF
Identical resistance of resistance R are connected as in figure then find out net resistance between x and y.
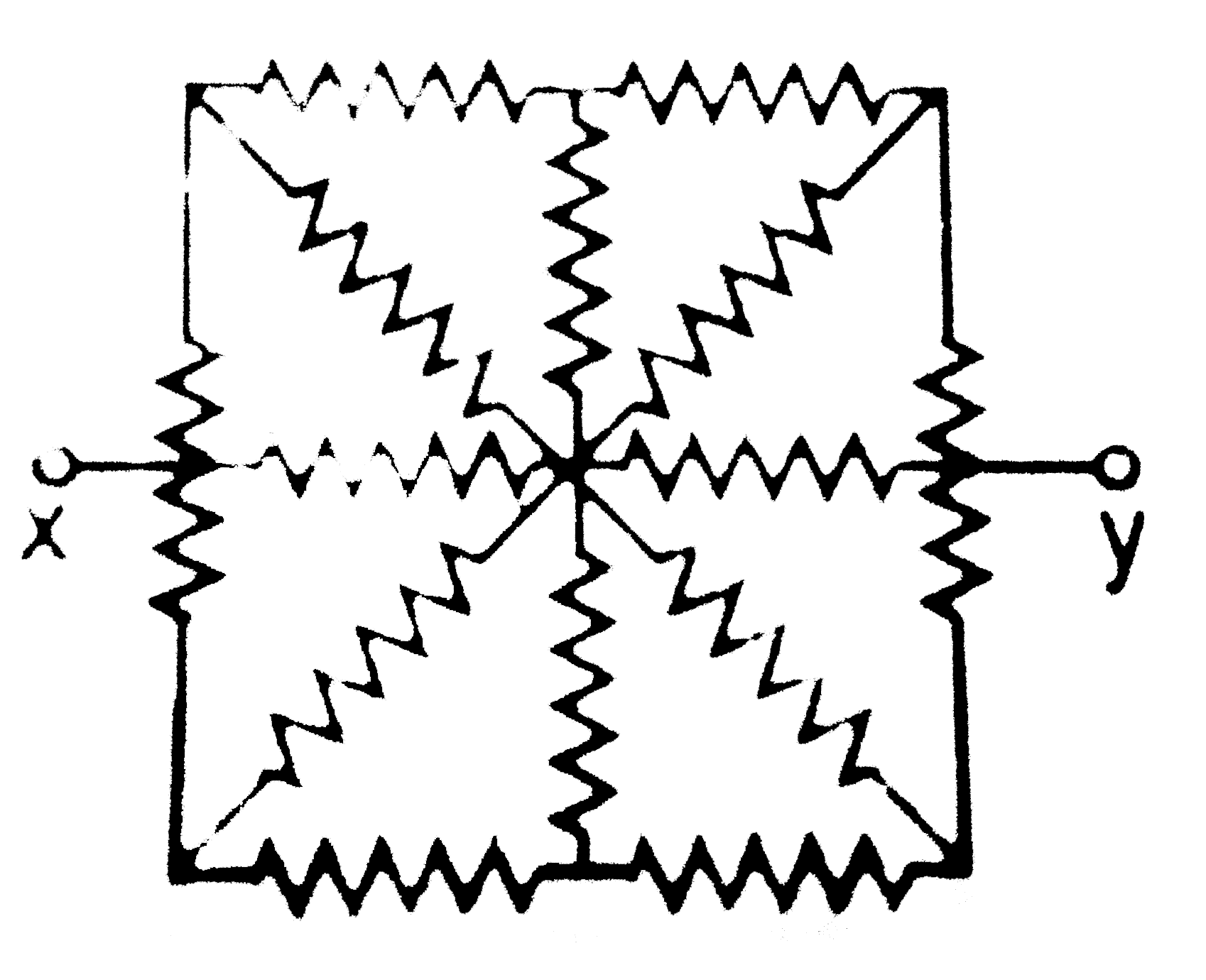
View SolutionThree identical resistors, each of resistance R, when connected in series with a d.c. source, dissipate power X. If the resistors are connected in parallel to the same d.c. source, how much power will be dissipated ?
View SolutionThree identical resistors, each of resistance R, when connected in series with a d.c. source, dissipata power X. if the resistors are connected in parallel to the same d.c. source, how much power will be dissipated?
View SolutionWhen resistors are connected in series, then net resistance_____
View SolutionThe equivalent resistance of three equal resistances connected in series is 27Ω. There equivalent resistance when connected in parallel is
View Solution
