A shell fired from the ground is just able to cross in a horizontal direction the top of a wall 90m away and 45m high. The direction of projection of the shell will be:
25∘
30∘
45∘
none of these
The correct Answer is:c
To solve the problem of finding the direction of projection of a shell that just crosses the top of a wall, we can follow these steps:
Step 1: Understand the problem
We have a wall that is 90 meters away from the point of projection and 45 meters high. We need to find the angle of projection (θ) of the shell.
Step 2: Use the maximum height formula
The maximum height (H) reached by a projectile is given by the formula:
H=u2sin2θ2g
where:
- H=45 m (height of the wall)
- u = initial velocity of the shell
- g=9.81m/s2 (acceleration due to gravity)
Step 3: Use the range formula
The range (R) of a projectile is given by:
R=u2sin2θg
In this case, the horizontal distance to the wall is 90 m, so:
R=90m
Step 4: Relate the maximum height and range
Since the wall is at half the range (45 m), we can express the maximum height in terms of the range:
H=u2sin2θ2g
Substituting R=90:
R=2H
This means:
90=u2sin2θg
Step 5: Set up the equations
From the maximum height equation:
45=u2sin2θ2g
From the range equation:
90=u2sin2θg
Step 6: Solve for u2
From the maximum height equation:
u2=90gsin2θ
From the height equation:
u2=90gsin2θ
Step 7: Equate and simplify
Setting the two expressions for u2 equal:
90gsin2θ=90g⋅sin2θ2g
Canceling 90g from both sides:
1=sin2θ2
Thus:
sin2θ=2
This is incorrect, so we need to check our calculations.
Step 8: Use the relationship between sin and tan
Using the relationship:
tanθ=Hd=4590=12
Thus:
θ=tan−1(12)
Step 9: Calculate the angle
Using a calculator:
θ≈26.57∘
Conclusion
The direction of projection of the shell will be approximately 26.57∘ above the horizontal.
---
We have a wall that is 90 meters away from the point of projection and 45 meters high. We need to find the angle of projection (θ) of the shell.
The maximum height (H) reached by a projectile is given by the formula:
H=u2sin2θ2g
where:
- H=45 m (height of the wall)
- u = initial velocity of the shell
- g=9.81m/s2 (acceleration due to gravity)
The range (R) of a projectile is given by:
R=u2sin2θg
In this case, the horizontal distance to the wall is 90 m, so:
R=90m
Since the wall is at half the range (45 m), we can express the maximum height in terms of the range:
H=u2sin2θ2g
Substituting R=90:
R=2H
This means:
90=u2sin2θg
From the maximum height equation:
45=u2sin2θ2g
From the range equation:
90=u2sin2θg
From the maximum height equation:
u2=90gsin2θ
From the height equation:
u2=90gsin2θ
Setting the two expressions for u2 equal:
90gsin2θ=90g⋅sin2θ2g
Canceling 90g from both sides:
1=sin2θ2
Thus:
sin2θ=2
This is incorrect, so we need to check our calculations.
Using the relationship:
tanθ=Hd=4590=12
Thus:
θ=tan−1(12)
Using a calculator:
θ≈26.57∘
The direction of projection of the shell will be approximately 26.57∘ above the horizontal.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projectile From A Height And Movingframe19videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projection From Inclined Plane20videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration15videos
MOCK TEST
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
Similar Questions
A gun kept on a striaght horizontal is used to hit a car, traveling along the same road away form the gun with a unfrom speed 20m/s. The car is at a distance 0f 160m from the gun, when the gun is fired at an angle of 45∘ with the horizontal Find the distance of the car from the gun when the shell hits it and the speed of projection of the shell from the gun.
View SolutionA ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall the angle of projection of ball is :-
View Solution
Knowledge Check
- Question 1 - Select One
A shell fired from the ground is just able to cross horizontally the top of a wall 90m away and 45m high. The direction of projection of the shell will be.
A25∘B30∘C60∘D45∘ - Question 2 - Select One
A ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
Aα=tan−1(13)Bα=tan−1(2)Cα=tan−1(23)Dα=tan−1(24) - Question 3 - Select One
A ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall, the angle of projection of ball is
Atan−1(32)Btan−1(23)Ctan−1(12)Dtan−1(34)
A stone is projected from the ground with velocity 25m/s . Two seconds later, it just clears a wall 5 m high. The angle of projection of the stone is (g=10m/sec2)
View SolutionA particle projected from the level ground just clears in its ascent a wall 30m high and 120√3 away measured horizontally.The time since projection to clear the wall is two second.It will strike the ground in the same horizontal plane from the wall on the other side of a distance of (in metres)
View SolutionA shell is fired with a horizontal velocity in the positive x direction from the top of an 80 m high cliff. The shell strikes the ground 1330 m from the base of the cliff. The drawing is not to scale.
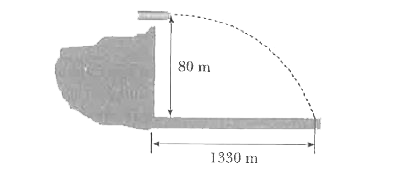
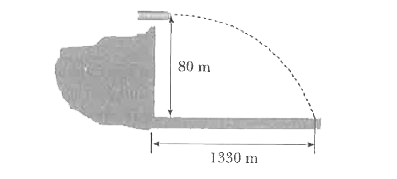
What is the speed of the shell as it hits the ground?View SolutionA shell is fired with a horizontal velocity in the positive x direction from the top of an 80 m high cliff. The shell strikes the ground 1330 m from the base of the cliff. The drawing is not to scale.
What is the magnitude of the acceleration of the shell just before is strikes the ground?View SolutionThe velocity and direction of projection of a shot which passes in horizontal direction just over the top of a wall which is 50 yds. away and 75 feet high.
View Solution

