A simple apparatus for demonstrating resonance in an air column is depicted in Fig. 7.59.A vertical pipe open at both ends is partially submerge in water , and a tuning fork vibration at an unknown frequency is placed near the top of the pipe . The length L of the air column can be adjusted by moving the pipe vertically . The sound waves generated by the fork are reinforced of the pipe . For a certain pipe , the smallest value of L for which a peak occurs in the intensity is 9.00cm.
a. What is the frequency of the tuning fork ?
b. What are the values of L for the next two resonance conditions? 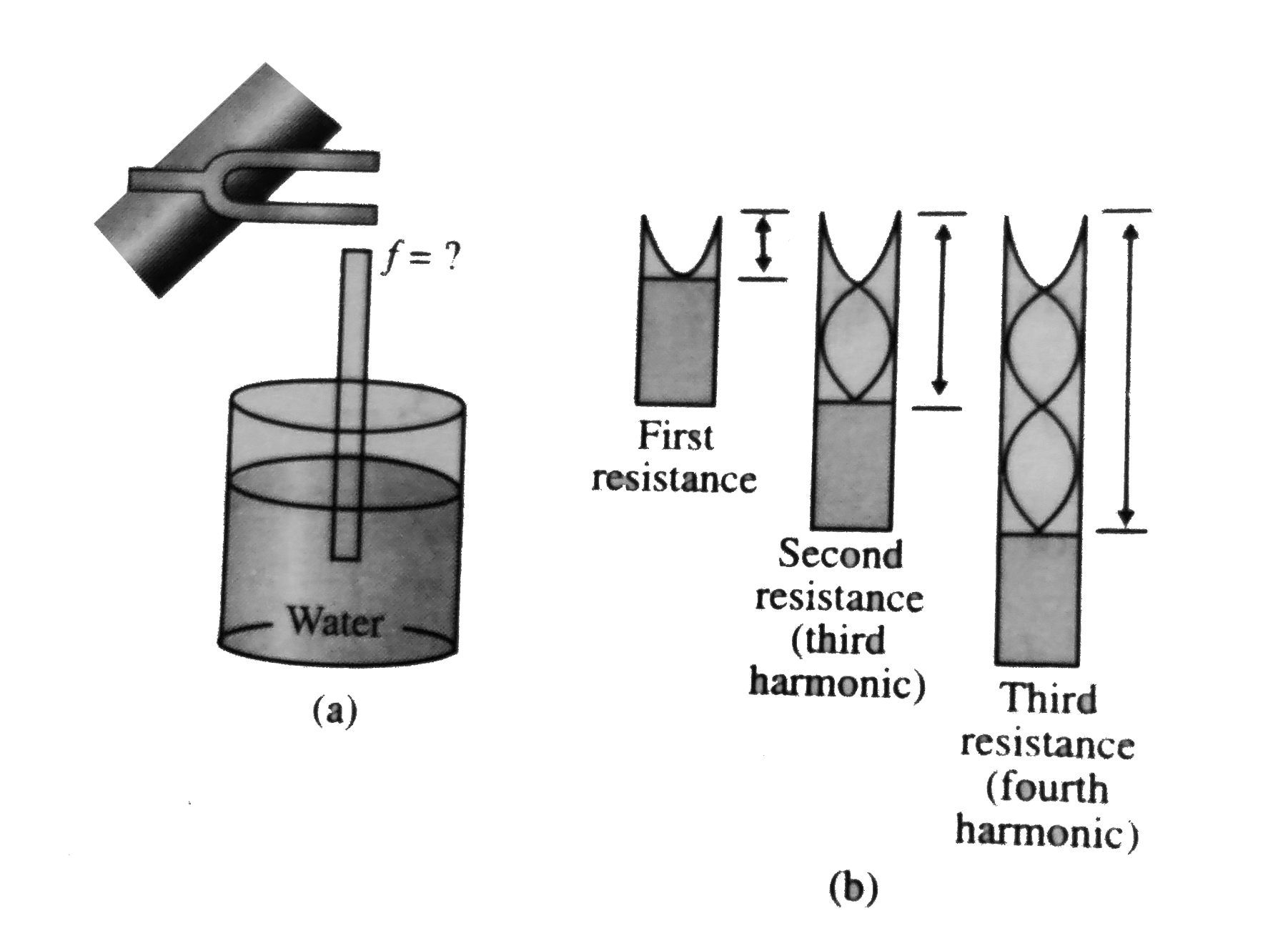
Consider how this problem differs from the preceding problem. In the culvert , the length was fixed and the air column was presented with a mixture of many frequencies . The pipe in this example is presented with one single frequency from the tuning fork , and the lenght of the pipe is varied until resonance is achieved.
This example is a simple substitution problem . Although the pipe is open at its lower end to allow the water to enter , the water's surface acts like a barrier . Therefore , this setup can be modelled as an air column closed at one end .
The fundamental frequency for L=0.090m:
f1=v4L=343m/s(4(0.090m))=953Hz
Because the tuning fork causes the air column to resonate at this frequency , this frequency must also be that of the tuning fork.
b. Use equation v=λf to find the wavelength of the sound wave from the tuning fork.
λ=vf=343m/s953Hz=0.360m
Notice from Fig. 7.59 (b) that the length of the air column for the second resonance is 3λ/4.
L=3λ/4=0.270m
Notice from Fig. 7.59(b) that the length of the air column for the third resonance is 5λ/4
L=5λ/4=0.450m
Similar Questions
A vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
Frequency of the tuning fork is
View SolutionA vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
Length of air column for third resonance will be
View Solution
Knowledge Check
A vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
Frequency of the tuning fork isA1072HzB940HzC860HzD533HzA vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
Frequency of the second overtone isA3400HzB2500HzC4300HzD1720HzsThe air in a pipe closed at one end is in resonance with a vibrating tuning fork of frequency 170 Hz. If the velocity of sound in air is 340 m/s, the length of the vibrating air column is
A100 cmB50 cmC300 cmD25 cm
A vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves traveling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm [ take speed of sound , v=344m/s].
Answer the following questions.
The air column here is closed at one end because the surface of water acts as a wall. Which of the following is correct ?
View SolutionA tuning fork of frequency n resonates with a closed organ pipe when the length of the shortest air columns are a and b respectively, then the speed of sound in air will be
View SolutionA vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
Length of air column for third resonance will be
View SolutionA vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
Length of air column for third resonance will be
View SolutionA vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
The air column here is closed at one end because the surface of water acts as a wall. Which of the following is correct ?
View Solution
