A simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
Tmax=mg[1+(Al)2]
Tmax=mg[1−(Al)2]
Tmax=mg[1−(lA)2]
Tmax=mg[1+(lA)2]
The correct Answer is:A
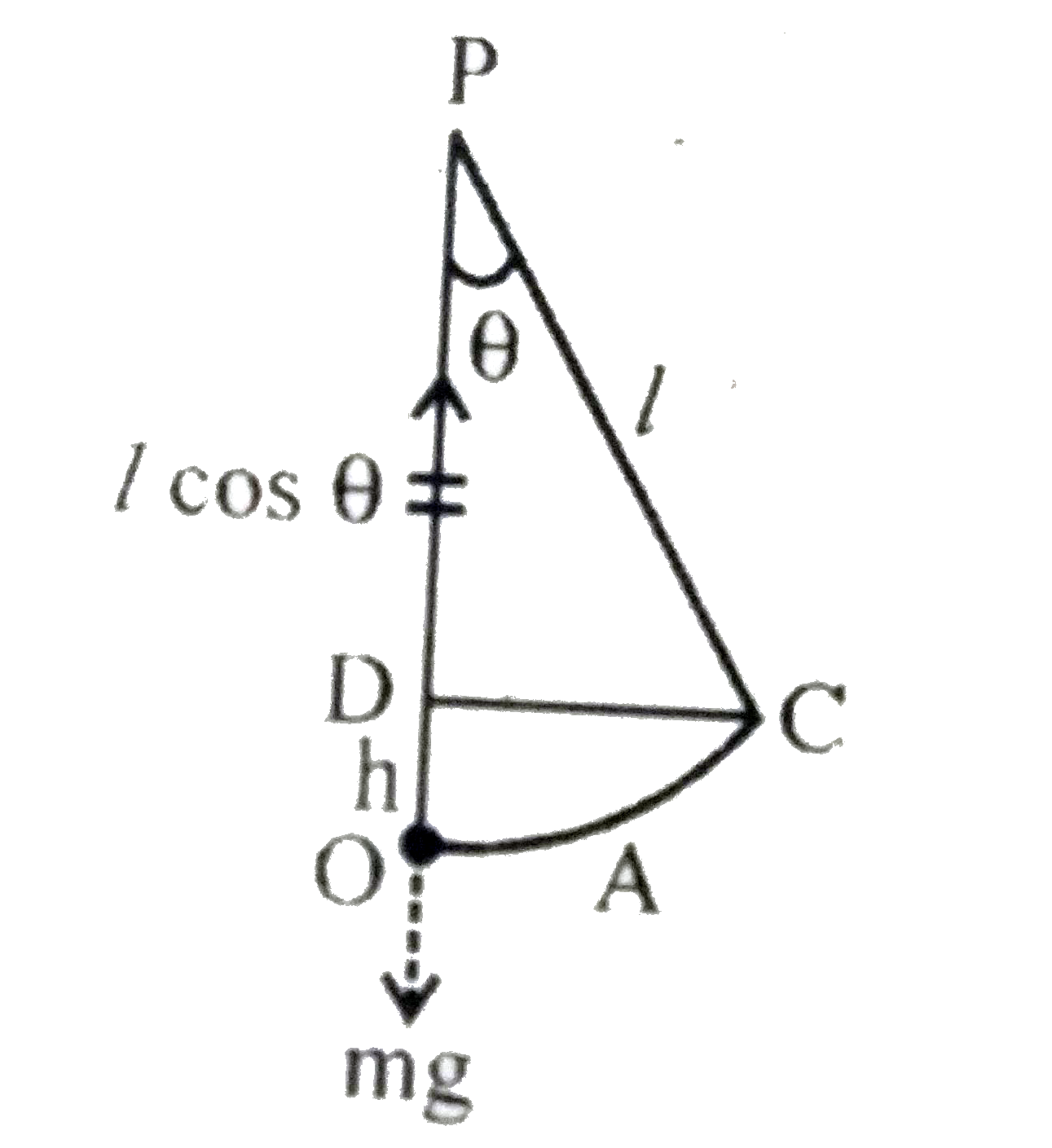
The tension in the string is maximum, when the bob is at the equilibrium position O. It is moving in a circle of radius r = l.
Tmax=mg+mv2r
When it is at C, its total energy (EC)= mgh and when it is at O its total energy (EO)=K.E.=12mv2
∵EC=EO∴mgh=12mv2∴v2=2gh
U"sin"g (2) in (1), we get
Tmax=mg+m(2gh)l(∵r=l)
=mg(1+2hl)
From the figure,
h=l−lcosθ=l(1−cosθ)=l.2sin2θ2
∵∠=arcradius
∴θ=OCl=Al(∵ arc = amplitude A)
∴θ2=A2l
and for small angles, sinθ=θ
∴sin2(θ2)=(A2l)2=A24l2
∴ from (4),h=l.2A24l2=A22l
∴2hl=2A22l.l=A2l2=(Al)2
U"sin"g (6) in (3), we get
Tmax=mg[1+(Al)2]
This is option (a).
Topper's Solved these Questions
Similar Questions
A simple pendulum having a bob of mass m undergoes smasll oscillastions with amplitude θ0 Find the tension in the string as a function of the angle made by the string with the vertical. When in this tension maximum, and when is it minimum?
View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View Solution
Knowledge Check
A simple pendulum has a string of length l and bob of mass m. When the bob is at its lowest position , it is given the minimum horizontal speed necessary for it to move in a circular path about the point point of suspension. The tension in the string at the lowest position if the bob is
A3mgB4mgC5mgD6mgA simple pendulam of length L carriers a bob of mass m. When the bob is at its lowest position, it is given the minimum horizontal speed necessary for it to move in a vertical circle about the point of suspension. When the string is horizontal the net force on the bob is
A√10mgB√5mgC4 mgD1 mgA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
AT=mgcosθ for all value of θBT=mgcosθ for only θ=ϕCT=mg,forθ=cos−1[13(2cosϕ+1)]DT will be larger for smaller values of θ
A simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30°. Then (g = 9.8 ms−2)
View SolutionA simple pendulum of length 'l' carries a bob of mass 'm'. If the breaking strength of the string is 3mg, the maximum angular amplitude from the vertical can be
View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
View SolutionA simple pendulum is oscillating with an angular amplitude 60∘. If mass of bob is 50 gram, then the tension in the string at mean position is (g=10ms−2)
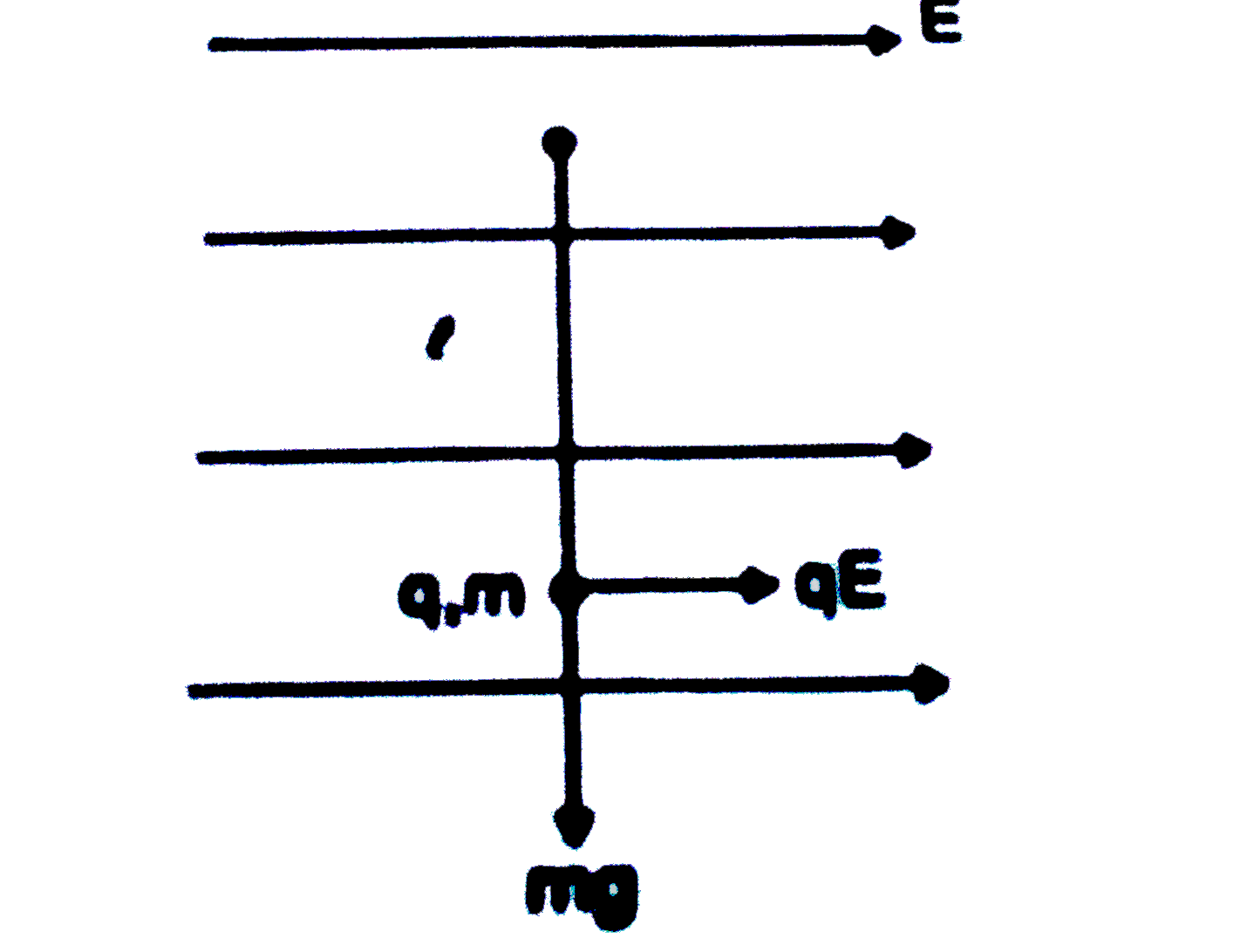
View SolutionA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
View Solution
