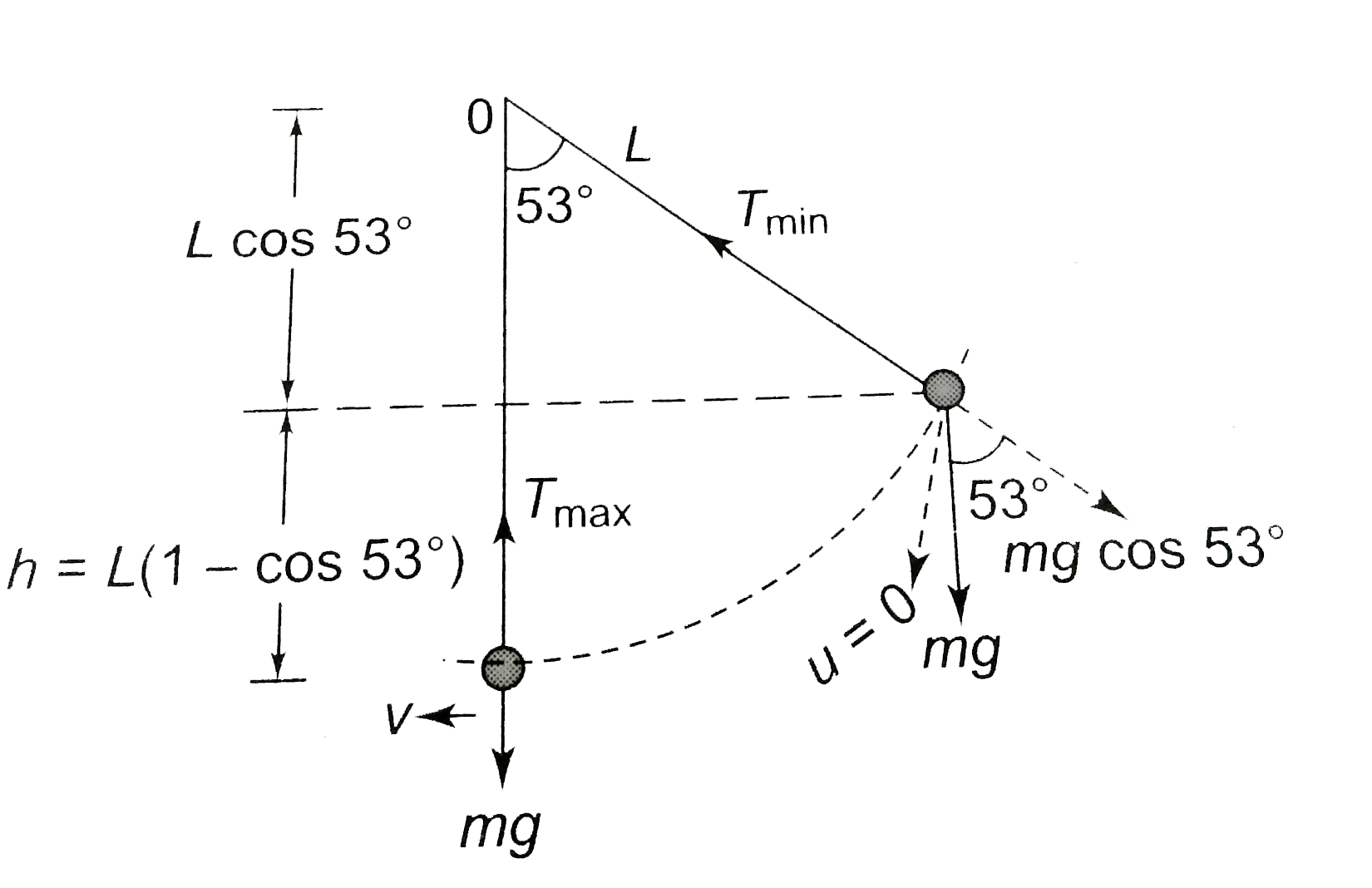
A simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
The tension in the string is minimum when the ball is at the highest point and maximum when the ball is at the lowest point.
v2=u2+2gh=0+2gL(1−cos53∘)
=2gL(1−3/5)=4gL5
Tmin−mgcos53∘=mu2L=0
Tmin−mg×35⇒Tmin=3mg5
Tmax−mg=mv2L=mL.4gL5
Tmax=mg+4mg5=9mg5
TminTmax=39=13
Topper's Solved these Questions
Similar Questions
AS simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes an angel of 370 with the verticl and is then released. Find the tension in the string when the bob is at its lowest position.

View SolutionWhen an archer pulls on the bow string with a force of 500 N, the bow string makes angles of 53∘ with the arrow. What is the tension in the string.
View Solution
Knowledge Check
A pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle θ with the vertical and released. Taking the suspension point as the axis, at the instant of release
Atorque on the pendulum is mgL cosθBtorque on the pendulum is mgL sinθCangular acceleration of pendulum is gcosθLDangular acceleration of pendulum is gsinθLA simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
At=2π√l/gBt=2π√lcosθ/gCT=4π2mlt2DThe bob is in equilibriumA simple pendulum consists of a ball of mass m suspended from the ceiling using a string of length L. The ball is displaced from its equilibrium position by a small angle θ. What is the magnitude of the restoring force that moves the toward its equilibrium position and produces simple harmonic motion?
AkxBmgCmg(cosθ)Dmg(sinθ)
A simple pendulum of length L having a bob of mass m is first taken aside so that the string forms the tight angle with the verticle and then released. The string hits a peg which is fixed at a distance below the point of suspension and the bob starts going in a circle centered at the peg. find the minimum value of y for which the bob goes in a complete circle about the peg.

View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionA mass of 10 kg is suspended from a spring balance, it is pulled aside by a horizontal string so that it makes an angle 60∘ with the vertical. The new reading of the balance is:
View SolutionA simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is

View SolutionA small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle 'a' with the vertical in equilibrium. Then the tension in the string is :
View Solution
