A simple pendulum is oscillating between extreme position P and Q about the mean position O. Wchi of the following statements are true about the motion of pendulum?
At point O, the acceleration of the bob is different from zero.
The acceleration of the bob is constant throughout the oscillation.
The tension in the string is contant throughout the oscillation.
The tension is maximum at O and minimum at P or Q.
The correct Answer is:A, D
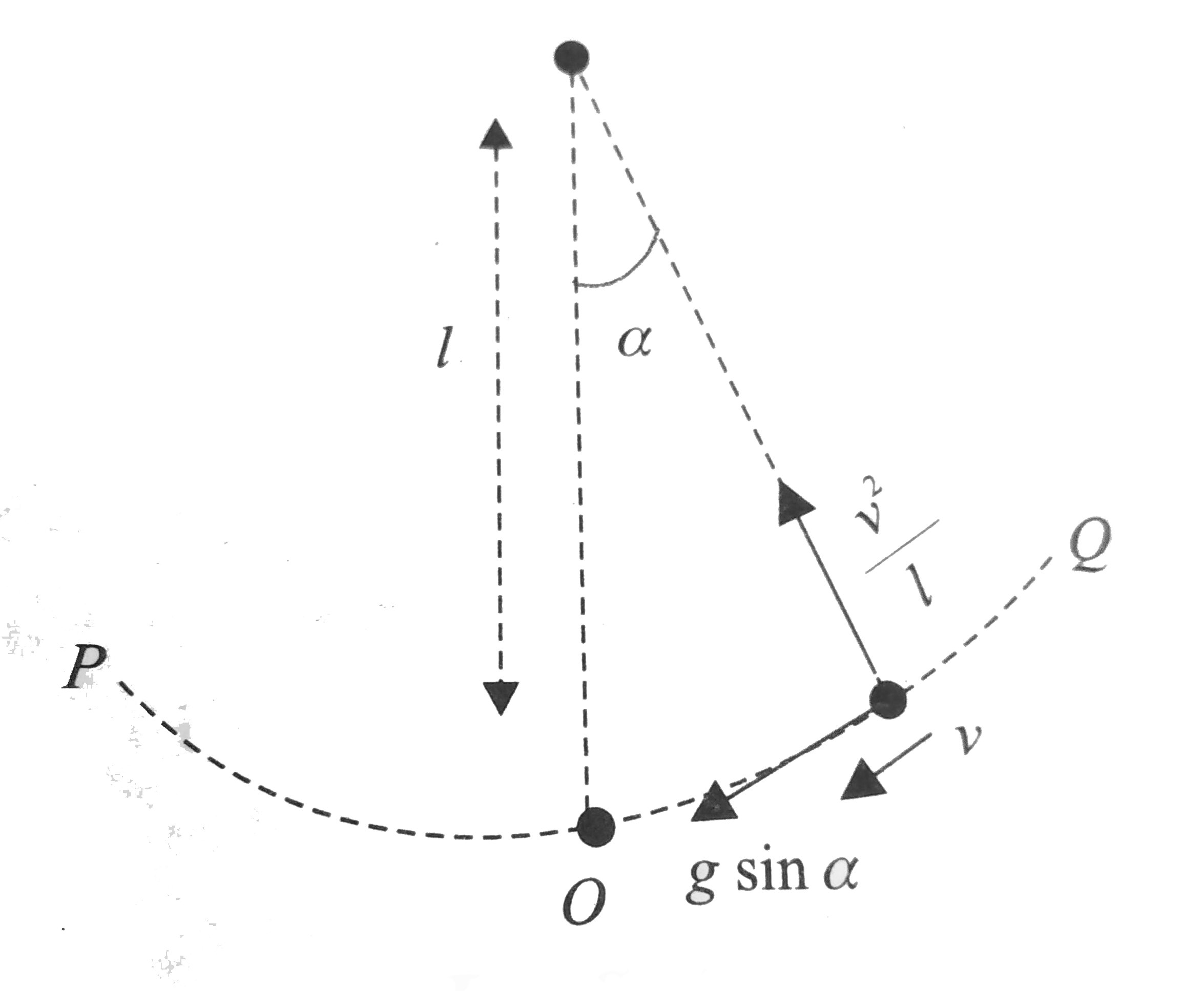
Statement (a) is correct. At any position O and P or between O and Q, there are two acceleration a tan gential acceleration gsinalphs and a centripetal acceleration v2l (because the pendulum moves along the arc of a circle or radiusl), where l is the length of the pendulum and v its speed at that position. When the bob is at the mean position O, the angle α=0, therefore sinα=0, hence the tengential acceleration is zero But at O, speed v is maximum and the centripetal acceleration v2l is directed radially towards the point of support. When the bob is at the end point P and Q, the speed v is zero, hence the centripetal acceleration is zero at the end point, but the tangential acceleration is maximum and is directed along the tangent to the curve at P and Q. The tension in the string is not contant throughout the oscillation. At any position between O and end point P or Q. The tension in the string is given by T=mgcosα.
At the end point P and Q, the value of α is the gretest, hence the tension is the least. At the mean position O, α=0 and α=1 which is the greatest, hence tension is greatest at the mean position.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Comprehension
Explore 33 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single Correct
Explore 107 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A simple pendulum is oscillating between two points A and B as shown in Figure 13.5. Is the motion of the bob uniform or non-uniform?
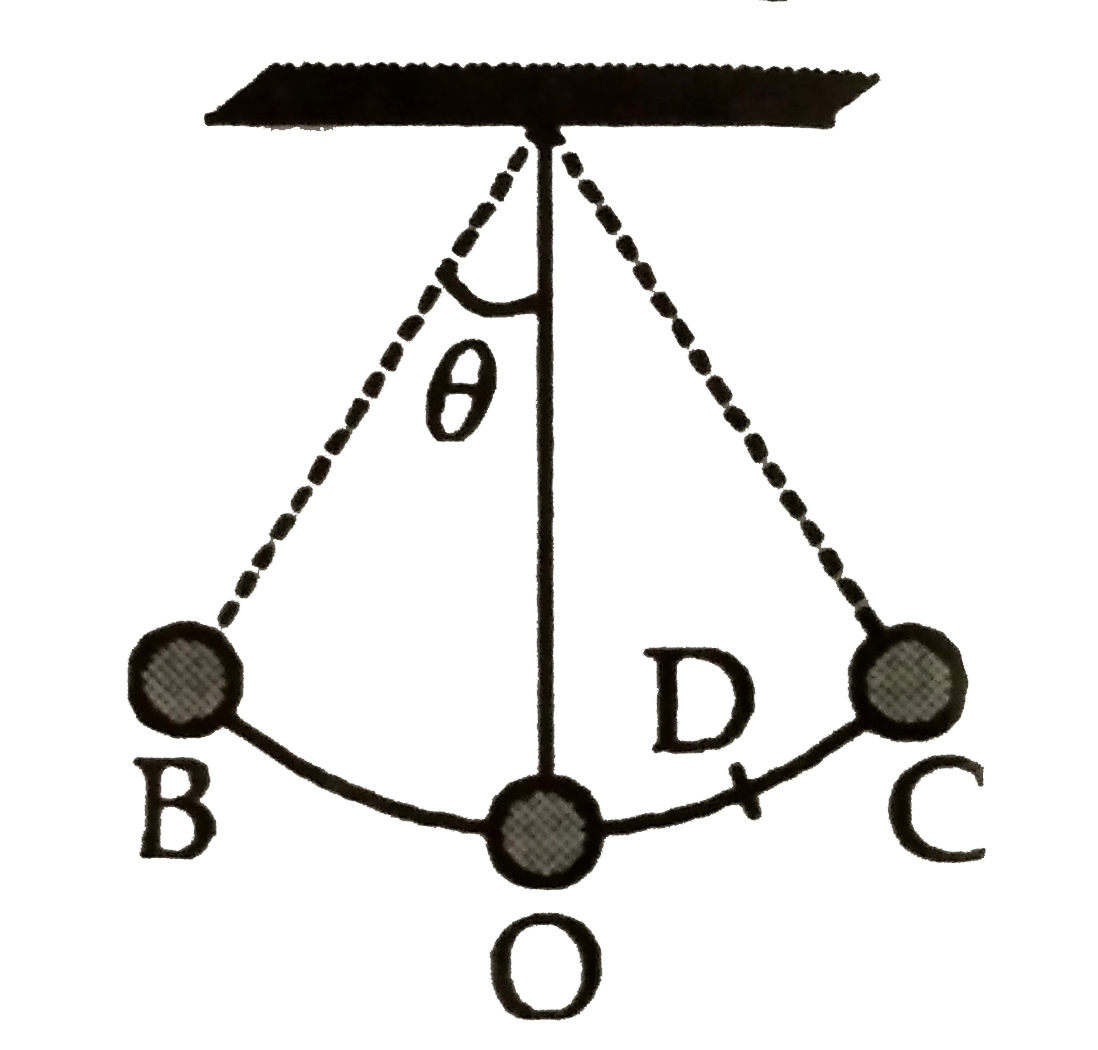
View SolutionA simple pendulum is moving simple harmonically with a period of 6 s between two extreme positions B and C about a point O. If the distance between B and C is 10 cm, then the time taken by the pendulum to move from position C to position D exactly midway between O and C will be
View Solution
Knowledge Check
A pendulum is oscillating about its mean position in vacuum. It has
Aonly kinetic energyBmaximum kinetic energy at extreme position,Cmaximum potential energy at its ·mean positionDsum of kinetic energy and potential energy remains constant throughout the motion.Which of the following statement is true for an oscillating simple pendulum?
APotential energy is minimum at maximum displacement positionBPotential energy is maximum at maximum displacement positionCKinetic energy is minimum at equilibrium position.DPotentail energy is maximum at equilibrium positionA simple pendulum executing SHM with a period of 6 s between two extreme positions B and C about a point O. if the length of the arc BC is 10 cm, how long will the pendulum take the move from position C to a position D towards O exactly midway between C and O?
A0.5 sB1 sC1.5 sD3 s
In a simple harmonic oscillator, at the mean position
View SolutionA simple pendulum oscillates in a vertical plane. When it passes through the mean position, the tension in the string is 3 times the weight of the pendulum bob.what is the maximum displacement of the pendulum with respect to the vertical
View SolutionIn simple harmonic motion, at the extreme positions
View SolutionIn. a simple harmonic oscillator, at the mean position
View SolutionAt mean position of an oscillating simple pendulum
View Solution