A sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
I2pRcosθ
12I2pR
4πI2pR
1πI2pR
The correct Answer is:B
To determine the power dissipated in a resistor when a sinusoidal AC current flows through it, we can follow these steps:
Step 1: Understand the relationship between peak current and average current
The peak current (Ip) is the maximum value of the sinusoidal current. The average (or effective) current (I_avg) for a sinusoidal waveform is given by:
Iavg=Ip√2
Step 2: Write the formula for power dissipated in a resistor
The power (P) dissipated in a resistor due to current flowing through it can be expressed as:
P=I2R
where I is the current flowing through the resistor.
Step 3: Substitute the average current into the power formula
Since we are dealing with AC current, we will use the average current calculated in Step 1:
P=(Iavg)2R=(Ip√2)2R
Step 4: Simplify the expression
Now, we simplify the expression:
P=(I2p2)R
Step 5: Final expression for power dissipated
Thus, the power dissipated in the resistor can be written as:
P=I2pR2
Conclusion
The power dissipated in the resistor when a sinusoidal AC current with peak current Ip flows through it is:
P=I2pR2
---
The peak current (Ip) is the maximum value of the sinusoidal current. The average (or effective) current (I_avg) for a sinusoidal waveform is given by:
Iavg=Ip√2
The power (P) dissipated in a resistor due to current flowing through it can be expressed as:
P=I2R
where I is the current flowing through the resistor.
Since we are dealing with AC current, we will use the average current calculated in Step 1:
P=(Iavg)2R=(Ip√2)2R
Now, we simplify the expression:
P=(I2p2)R
Thus, the power dissipated in the resistor can be written as:
P=I2pR2
The power dissipated in the resistor when a sinusoidal AC current with peak current Ip flows through it is:
P=I2pR2
Topper's Solved these Questions
Similar Questions
Knowledge Check
A sinusoidal A.C. current flows through a resistor of resistance R. If the peak current is IP, then the power dissipated is
AI2pRcosθB12I2pRC4πI2pRD1πI2pRA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
AI2PRcosθB12I20RC4πI2PRD1π2I2PRA sinusoidal A.C. current flows through a resistor of resistance 10Ω. If the peak current is 2A flowing through the resistor, then the power dissipated is_________W.
A30B20C10D40
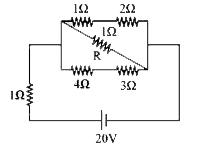
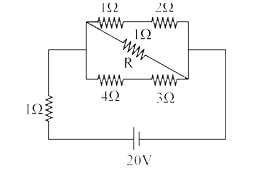
Find the current through resistor R.
View SolutionIn an AC circuit with voltage V and current I, the power dissipated is
View SolutionIn an a.c. circuit with voltage V and current I, the power dissipated is
View SolutionA sinusoidal alternating current of peak value (I0) passes through a heater of resistance R. What is the mean power output of the heater?
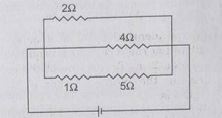
View SolutionA current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is
View Solution