A sinusoidal transverse wave is traveling on a string. Any point on the string
moves in the same direction as the wave.
moves in simple harmonic motion with a different frequency than that of the wave.
moves in simple harmonic motion with the same angular frequency as the wave
moves in uniform circular motion with a different angular speed than the wave.
The correct Answer is:C
To solve the problem regarding a sinusoidal transverse wave traveling on a string, we need to analyze the behavior of points on the string as the wave propagates. Here’s a step-by-step breakdown of the solution:
1. Understanding the Wave Motion:
- A sinusoidal transverse wave on a string means that the displacement of the string at any point varies sinusoidally with time. The wave travels along the string, causing points on the string to oscillate.
Hint: Visualize how a wave travels along a string, causing points to move up and down.
2. Equation of the Wave:
- The displacement y of a point on the string can be described by the equation:
y(x,t)=Asin(kx−ωt)
where A is the amplitude, k is the wave number, and ω is the angular frequency.
Hint: Remember that the sine function describes the oscillation of points on the string.
3. Motion of Points on the String:
- Each point on the string undergoes simple harmonic motion (SHM) about its equilibrium position. The frequency of this SHM is the same as the frequency of the wave.
Hint: Relate the frequency of the wave to the motion of points on the string.
4. Different Frequencies:
- If the problem states that points on the string move in SHM with a different frequency than that of the wave, this would be incorrect. All points on the string oscillate with the same frequency as the wave.
Hint: Consider the implications of different frequencies on the motion of points.
5. Angular Frequency:
- The angular frequency ω of the wave is the same for all points on the string. Therefore, any point on the string that oscillates in SHM must have the same angular frequency as the wave.
Hint: Recall that angular frequency is related to how quickly the oscillation occurs.
6. Conclusion:
- The only correct statement is that points on the string move in simple harmonic motion with the same angular frequency as that of the wave. This means that option C is correct.
Hint: Summarize the findings to identify the correct option.
Final Answer:
The correct option is C: Points on the string move in simple harmonic motion with the same angular frequency as that of the wave.
- A sinusoidal transverse wave on a string means that the displacement of the string at any point varies sinusoidally with time. The wave travels along the string, causing points on the string to oscillate.
- The displacement y of a point on the string can be described by the equation:
y(x,t)=Asin(kx−ωt)
where A is the amplitude, k is the wave number, and ω is the angular frequency.
- Each point on the string undergoes simple harmonic motion (SHM) about its equilibrium position. The frequency of this SHM is the same as the frequency of the wave.
- If the problem states that points on the string move in SHM with a different frequency than that of the wave, this would be incorrect. All points on the string oscillate with the same frequency as the wave.
- The angular frequency ω of the wave is the same for all points on the string. Therefore, any point on the string that oscillates in SHM must have the same angular frequency as the wave.
- The only correct statement is that points on the string move in simple harmonic motion with the same angular frequency as that of the wave. This means that option C is correct.
The correct option is C: Points on the string move in simple harmonic motion with the same angular frequency as that of the wave.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (More than One Coorect Choice Type)10videos
WAVES-I
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Linked Comprehension)8videos
WAVES-I
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Problems60videos
WAVES-I
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)5videos
WAVE - II
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
WORK, POWER, AND ENERGY
Similar Questions
A sinusoidal transverse wave travel on a string. The string has length 8.00m and mass 6.00g. The wave speed is 30.0m/s and the wavelength is 0.200m. (a) If the wave is to have an average power of 50.0W, what must be the amplitude of the wave? (b) For the same string, if the ampitude and wavelength are the same as in part (a) what is the average power for the wave if the tension is increased such that the wave speed is doubled?
View SolutionA transverse wave is travelling on a string and is governed by the equation y=2sin(ωt–kx). The wavelength for which wave velocity will be equal to maximum particle velocity is _____m.
View Solution
Knowledge Check
- Question 1 - Select One
A sinusoidal transverse progressive wave travelling on stretched string along x axis Choose appropriate number for direction of velocity and acceleration respectively force particle P shown in the diagram.
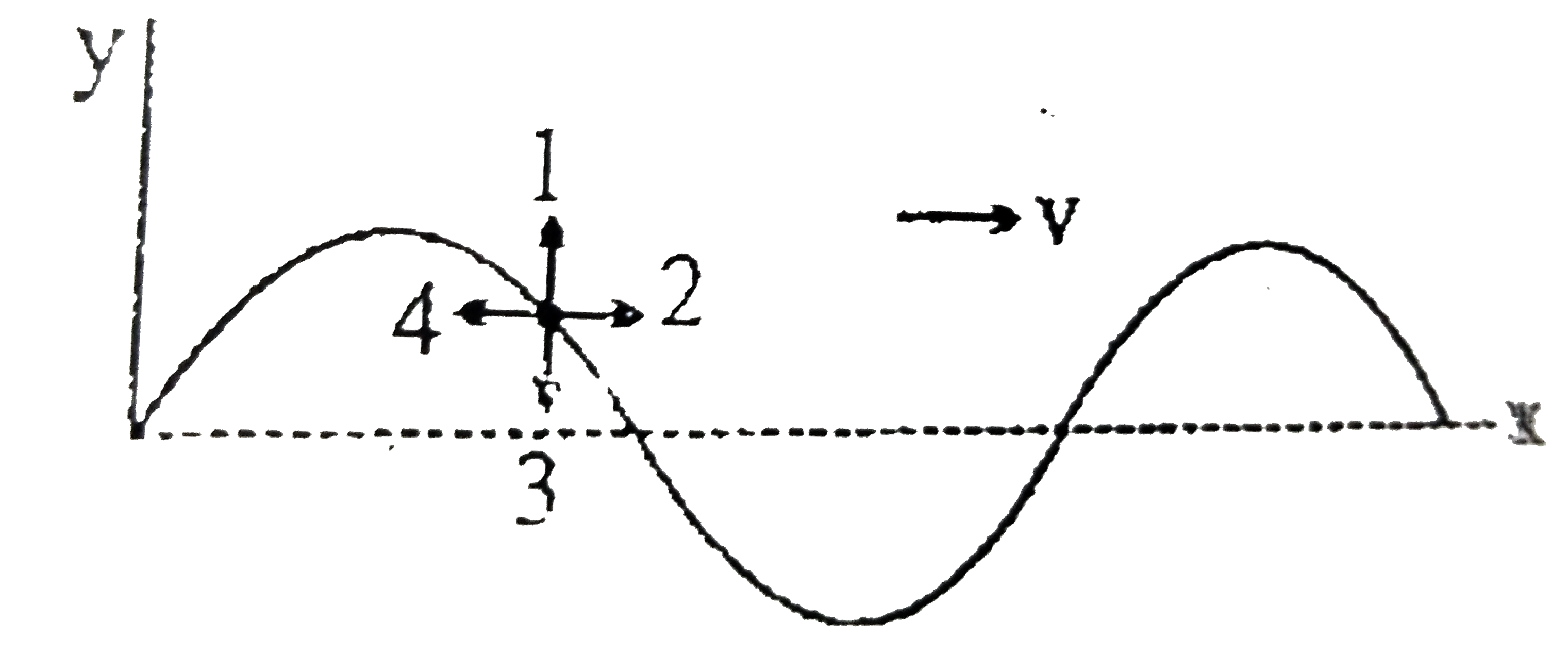A3 and 1B1 and 3C1 and 1D2 and 4 - Question 2 - Select One
A transverse wave is travelling along a string from left to right. The figure below represents the shape of the string at a given instant. At this instant the points have an upward velocity are (here X-wave displacement, Y- particle displacement)
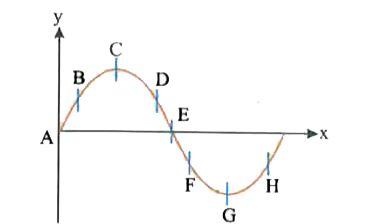AD,E,FBA,B,HCB,D,FDA,E,H - Question 3 - Select One
In case of a transverses wave in a string
Aif λ2π>A0 maximum particle speed is more than the wave speedBif λ2π=A0, particle speed is equal to the wave speedCif λ2π=A0, maximum particle speed is less than wave speedDif λ2π=A0, maximum particle speed may be greater than wave speed
The figure shows a transverse wave travelling in a string in negative x-axis direction. Three points A, B and C are indicated on the string at the instant shown
The correct statement(s) is/are.View SolutionA transverse wave is travelling along a horizontal string. The first figure is the shape of the string at an instant of time. The second picture is a graph of the vertical displacement of a point on the string as a function of time. How far does this wave travel along the string in one second?
, View SolutionA string of length 2L, obeying Hooke's Law, is stretched so that its extension is L. The speed of the tranverse wave travelling on the string is v. if the string is futher stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionA transverse waves is travelling in a string. Study following statement.
(i) Equation of the wave is equal to the shape of the string at an instant t. (ii) Equation of thhe wave is general equation for displacement of a particle of the string (iii) Equation of the wave must be sinusoidal equation (iv) Equation of the wave is an equation for displacement of the particle at one end only.correct statement areView SolutionA wave is travelling along a string. At an instant shape of the string is as shown in the enclosed figure. At this instant, point A is moving upwards. Which of the following statements are correct?
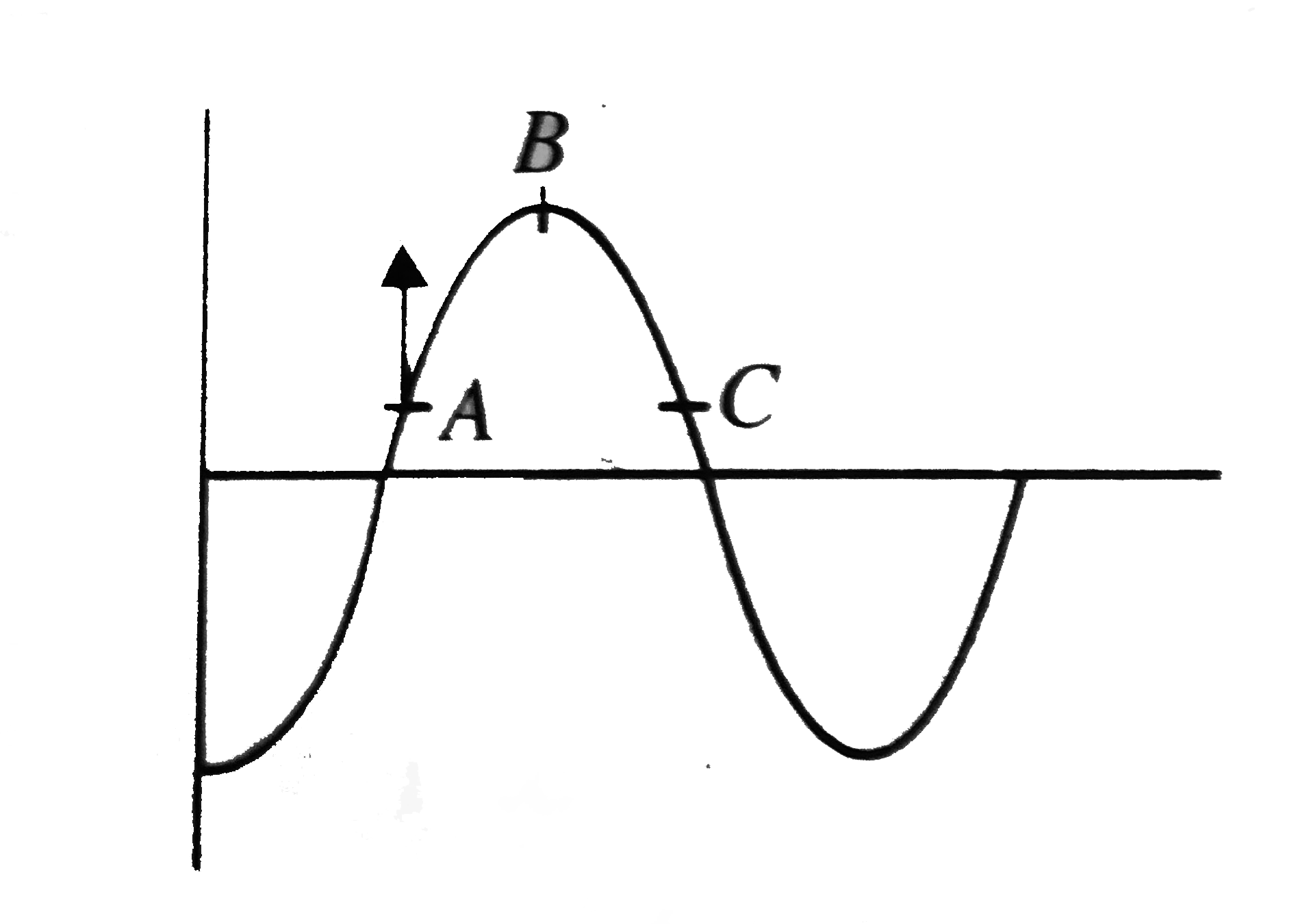
View Solution