A slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
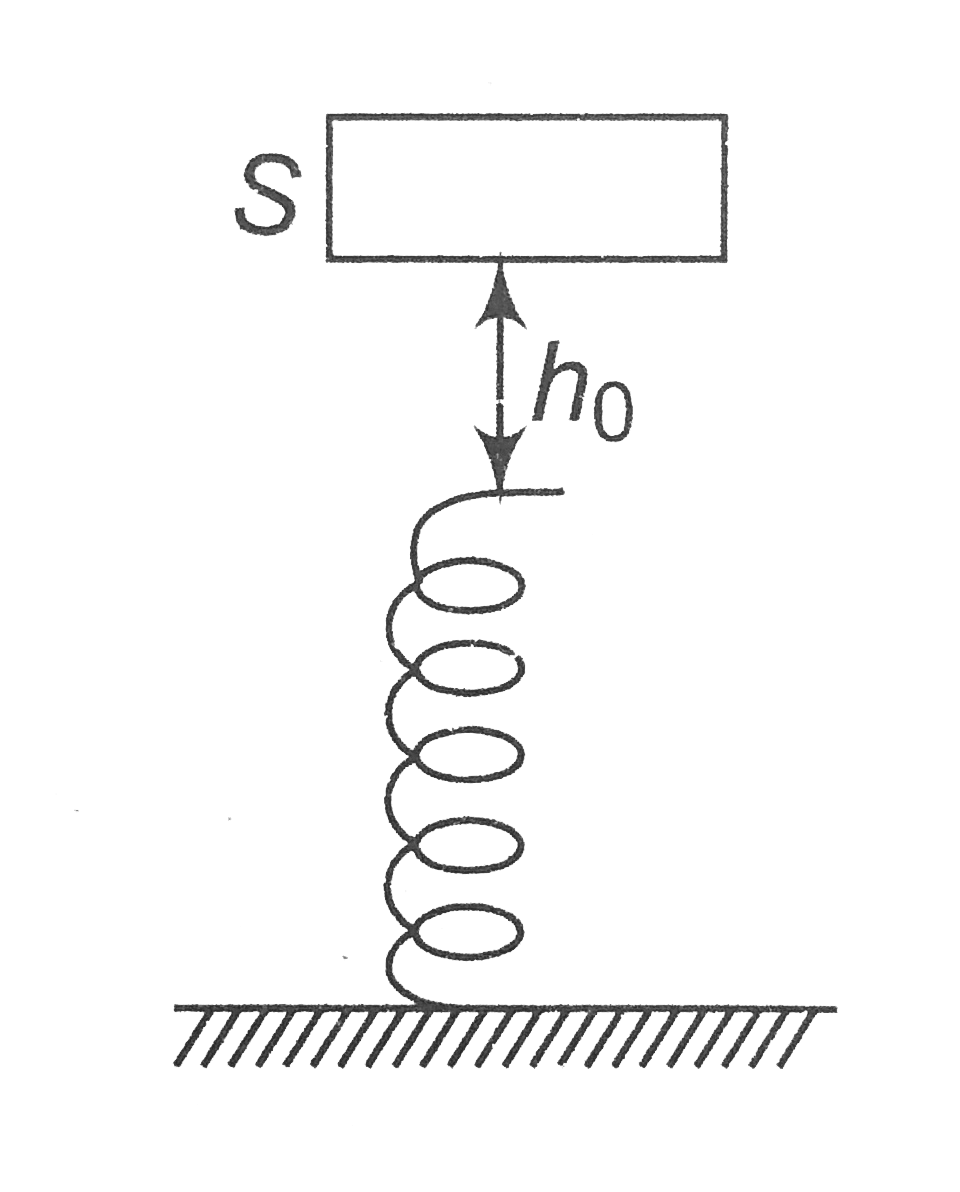
mgh0=12kx2
mg(h0−x)=12kx2
mgh0=12k(h0+x)2
mg(h0+x)=12kx2
The correct Answer is:D
Equate loss of gravitational potential energy with gain of elastic potential energy.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power
25 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Circular Motion In Vertical Plane
21 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Potential Energy, Conservative And Non-Conservative Forces
28 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
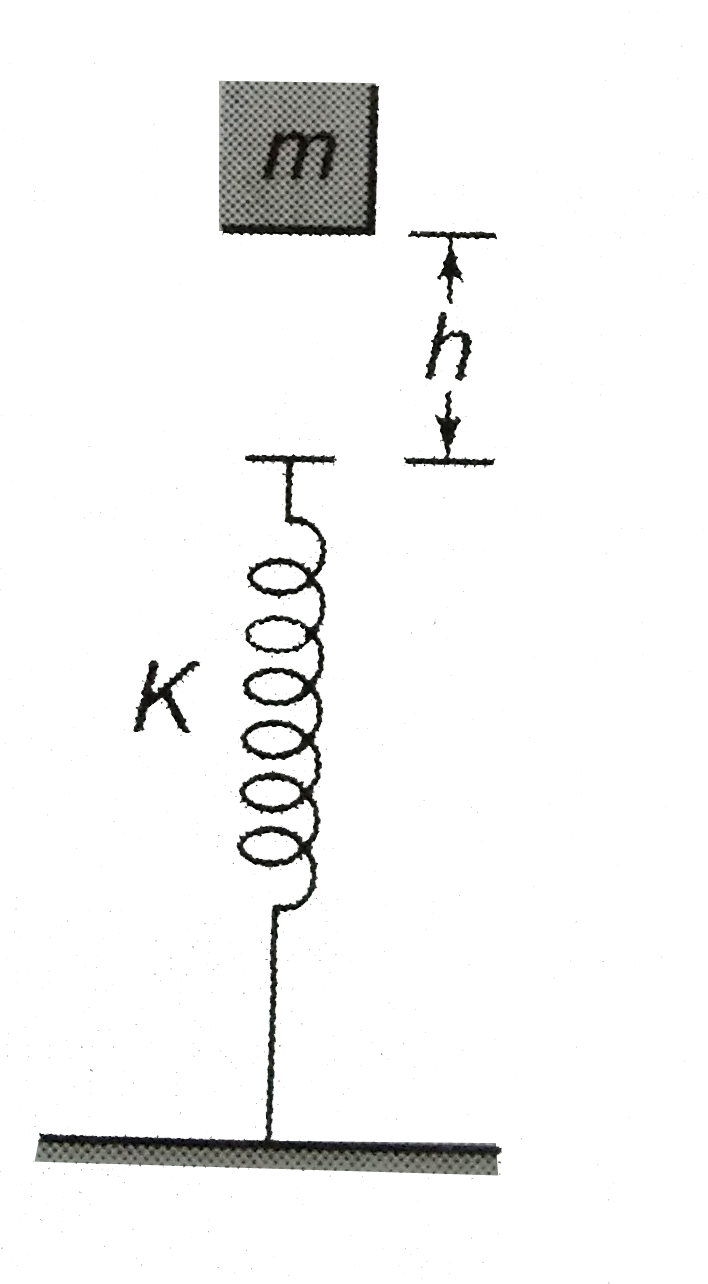
A block is released from height h, find the maximum compression of spring of spring constant k.
View SolutionA smooth block of mass m is released from rest from a height h. It slides and compresses the spring of stiffness k. Find the maximum compression of the spring .
Taking block spring a system. Now external force is doing work on system and no non-conservative force is present. The mechanincal energy should be conserved.
ΔK+ΔU=0
View Solution
Knowledge Check

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2Find maximum compression is the spring from the given figure.
 A√25mB16√25mC3√25mD6√25m
A√25mB16√25mC3√25mD6√25mA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
Amgk√1−2hkmgBmgkCmgk+mgk√1+2hkmgDmgk−mgk√1−2hkmg
A block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

View SolutionA block of mass 2kg is propped from a height of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
View Solution
