A slender rod of mass $m$ and length $L$ is pivoted about a horizontal axis through one end and released from rest at an angle of $30^{\circ}$ above the horizontal. The force exerted by the pivot on the rod at the instant when the rod passes through a horizontal position is

A

$\sqrt{\frac{10}{4}}$ mg along horizontal

B

$m g$ along vertical

C

$\frac{\sqrt{10}}{4} m g$ alonng a line making an angle of ${tan}^{- 1} (\frac{1}{3})$ with the horizontal

D

$\frac{\sqrt{10}}{4}$ mg along a line making an angle of ${tan}^{- 1} (3)$ with the horizontal

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The angular velocity oif the rod about the pivot when is passes through the horizontal position is given by

$m g \times \frac{L}{2} {sin 30}^{\circ} = \frac{m L^{2}}{3} \times \frac{ω^{2}}{2}$
$ω = (\frac{3 g}{2 L})$
Radial acceleration of the centre of mass (as centre of mass is moving in a circle of radius $L / 2$ ) is given
$a_{r} = ω^{2} \frac{L}{2} = \frac{3 a}{4}$
Torque about pivot, in the horizontal position, is $τ = m g \frac{L}{2} = I α$
$α = \frac{m g L / 2}{m L^{2} / 3 = \frac{3 g}{2 L}}$
Tangential acceleration of the centre of mass $a_{t} = \frac{L}{2} α = \frac{3 g}{4}$
Draw the $F B D$ of the rod at an instant when it passes through the horizontal position. Use Newton's second law of equation.

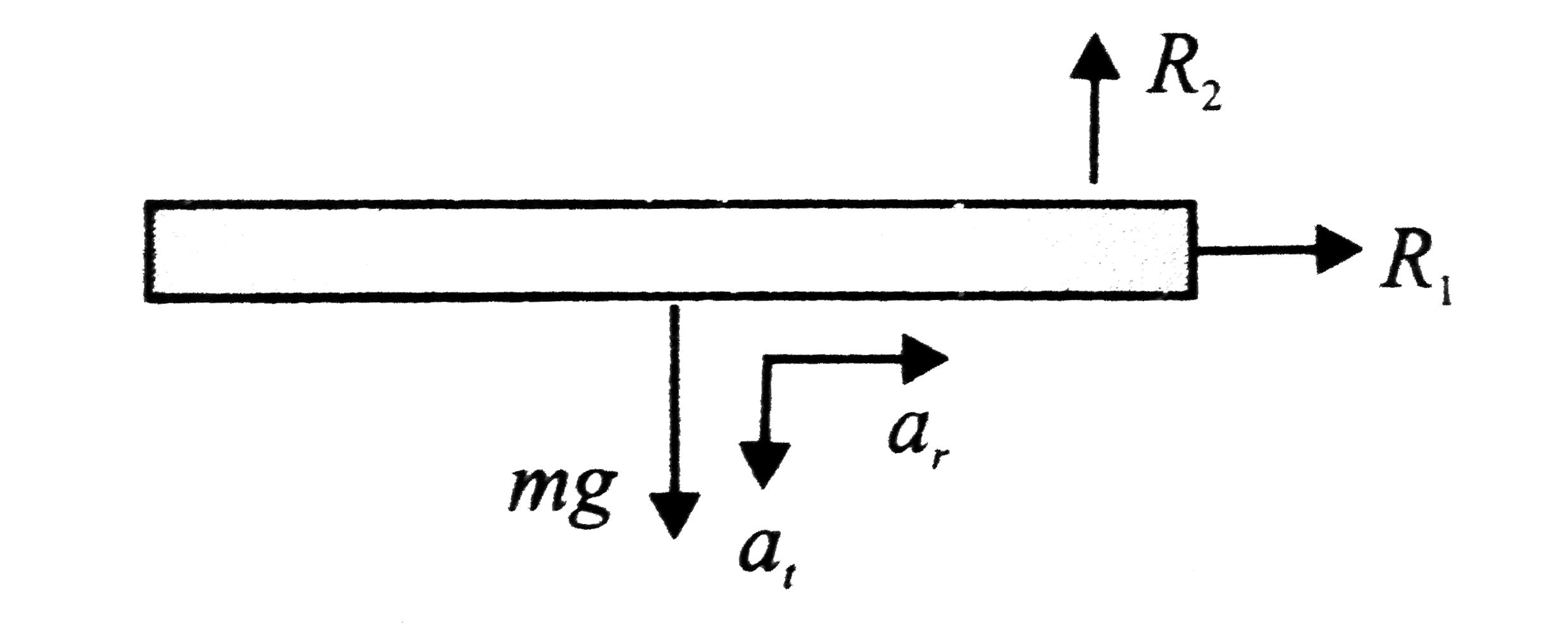
$R_{1} = m a_{r} = \frac{3 m g}{4}$
$m g - R_{2} = m \times a_{t} = \frac{3 m g}{4}$
$R_{2} = \frac{m g}{4}$
So, reaction force by the pivot on the rod $R = R_{1}^{2} + R_{2}^{2} = \sqrt{10} m \frac{g}{4}$ at angle of ${tan}^{- 1} (R_{2} / R_{1}) = [= {tan}^{- 1} (\frac{1}{3})]$ with the horizontal.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 1-Single Correct

Home
Ask Doubt
Profile