A small ball is projected horizontally between two large blocks. The ball is given a velocity Vms−1 and each of the large blocks move uniformly with a velocity of 2Vms−1. The ball collides elastically with the blocks. If the velocity of the blocks do not change due to the collision, then find out the velocity of the ball after the 2nd collision.
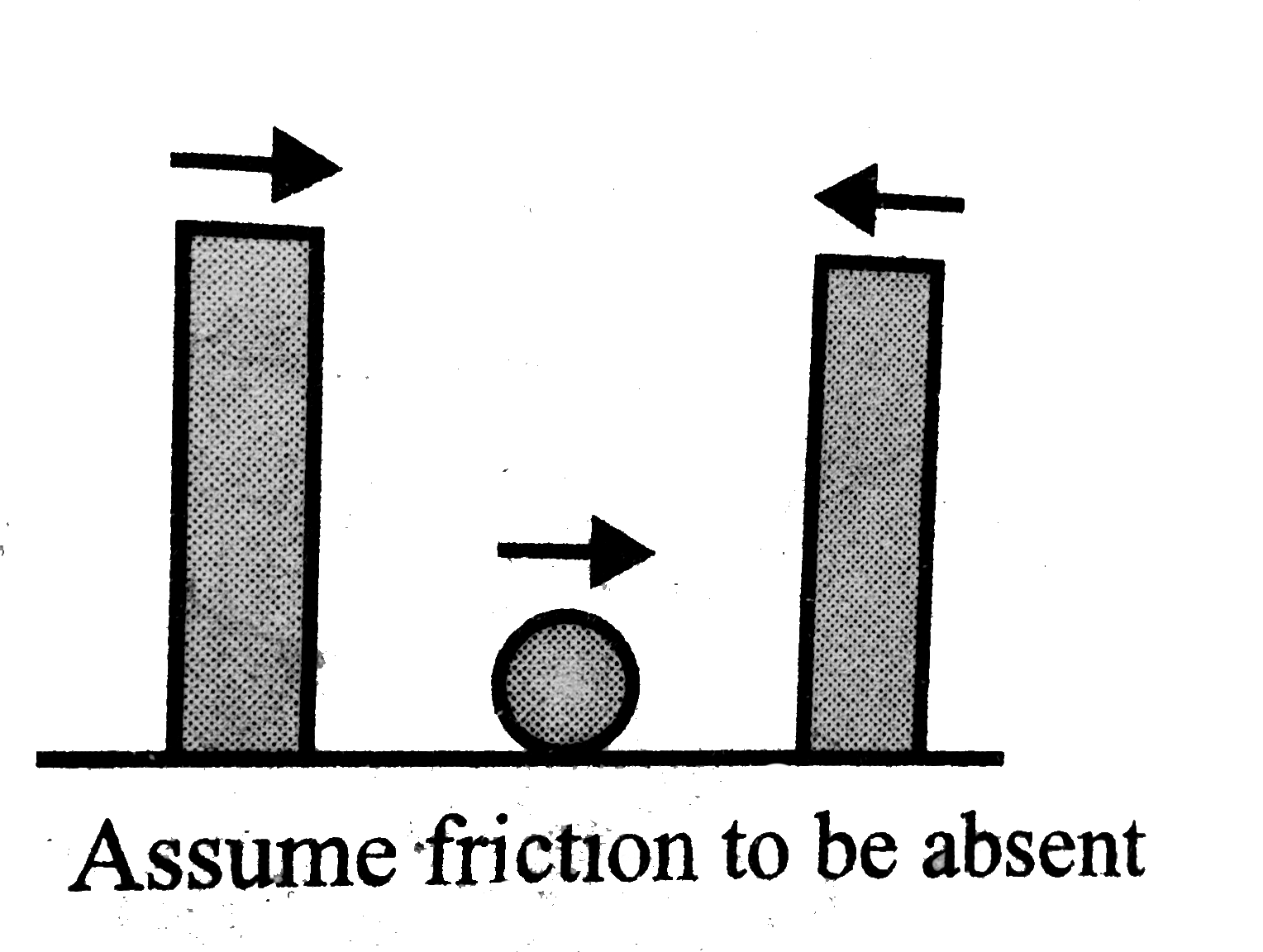
5v
7V
9V
none of these
The correct Answer is:C
Use the following result
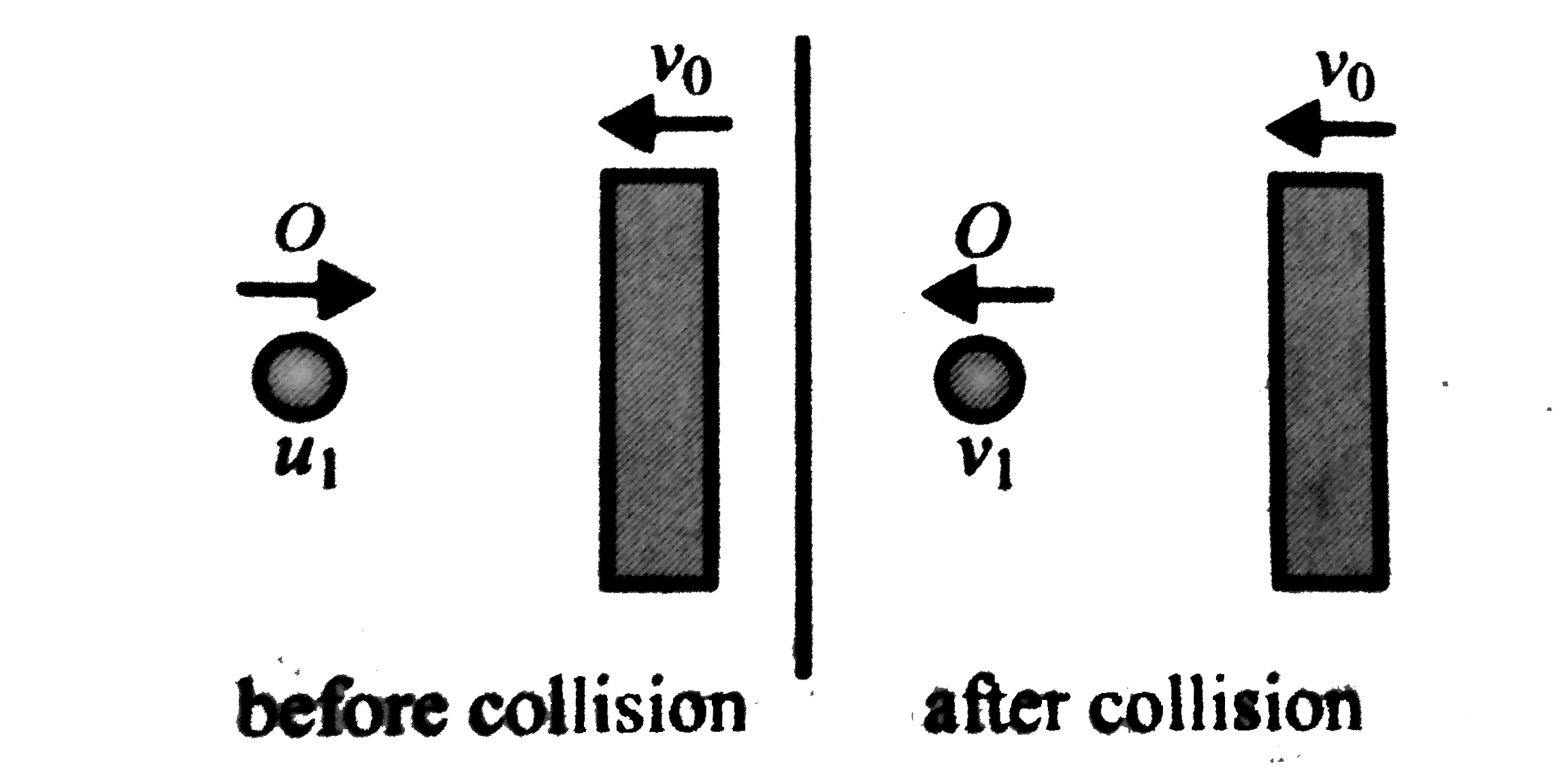
e=v2−v1u1−u2⇒1=−v0(−v1)u1−(−v0)⇒v1u1+2v0
using the above result
Now velocity after first collision
V'=V+2(2V)=5V
Velocity after second collision
V''=V'+2(2V)=5V+4V=9V
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA ball is projected horizontally from a tower with a velocity of 4ms−1. Find the velocity of the ball after 0.7 s. Take g=10ms−2.
View Solution
Knowledge Check
A truck moving on horizontal road east with velocity 20ms–1 collides elastically with a light ball moving with velocity 25ms–1 along west. The velocity of the ball just after collision
A65 ms–1 towards eastB25 ms–1 towards wastC65 ms–1 towards wastD20 ms–1 towards eastA wall moving with velocity 2cms−1 towards the ball and ball is moving towards the wall with a velocity 10cms−1. It hits the wall normally and makes elastic collision with wall. The velocity of ball after collision with wall in cms−1.
A12B8C14D16A glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
A√e2a2+b2 at angle tan−1(aeb) to the verticalB√a2+e2b2 at angle tan−1(aeb) to the verticalC√a2+b2e2 at angle tan−1(eab) to the verticalD√a2e2+b2 at angle tan−1(aeb) to the vertical
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionIf a ball strikes with a velocity u1 at the wall which itself is approaching it with a velocity u2 then find the velocity of the ball after collision with the wall.
View SolutionA ball moving with a speed of 9ms−1 strikes an identical ball such that after the collision the direction of each ball makes and angle 30∘ with the original line of motion. Find the speeds of the two balls after the collision.
View SolutionThe ball A collides elastically with an identical ball B with a speed v. The ball B touches another identical ball C. The velocity of C, after the impact, is equal to
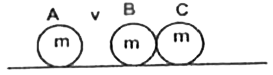
View SolutionA truck moving on horizontal road towards east with velocity 20ms1 collides elastically with a light ball moving with velocity 25ms−1 along west. The velocity of the ball just after collision
View Solution
