A small ball is pushed from a height h along a smooth hemispherical bowl of rodius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
√2gh
√2g(R+h)
√2g(R−h)
None of these
The correct Answer is:C
h'=R−h∴vmin=√2gh'⇒vmin=√2g(R−h)

Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A ball of mass m is released from rest from a height H along a smooth, light and fixed tube having a semicircular portion so that the ball just reaches the top of the semicircle.
a. Find the radius of the semi-circle.
b. Find the maximum force imparted by the ball on the ground.

View SolutionA small block is placed on the top of a smooth inverted hemispherical bowl of radius R.

(a) The bowl is given a sudden impulse so that it begins moving horizontally with speed V. Find minimum value of V so that the block immediately loses contact with the bowl as it begins to move. (b) The bowl is given a constant acceleration ‘a’ in horizontal direction. Find maximum value of ‘a’ so that the block does not lose contact with the bowl by the time it rotates through an angle θ=1∘ relative to the bowl. You can make suitable mathematical approximations justified for small value of angle θ.
View Solution
Knowledge Check
A small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.
A2:1B3:2C4:3D5:2A ball is relased from the top of a building 180m high. It takes time t to reach the ground With what speed should it be projected down so that it reaches the ground time 516.
A50ms−1B61ms−1C11ms−1D2ms−1A small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
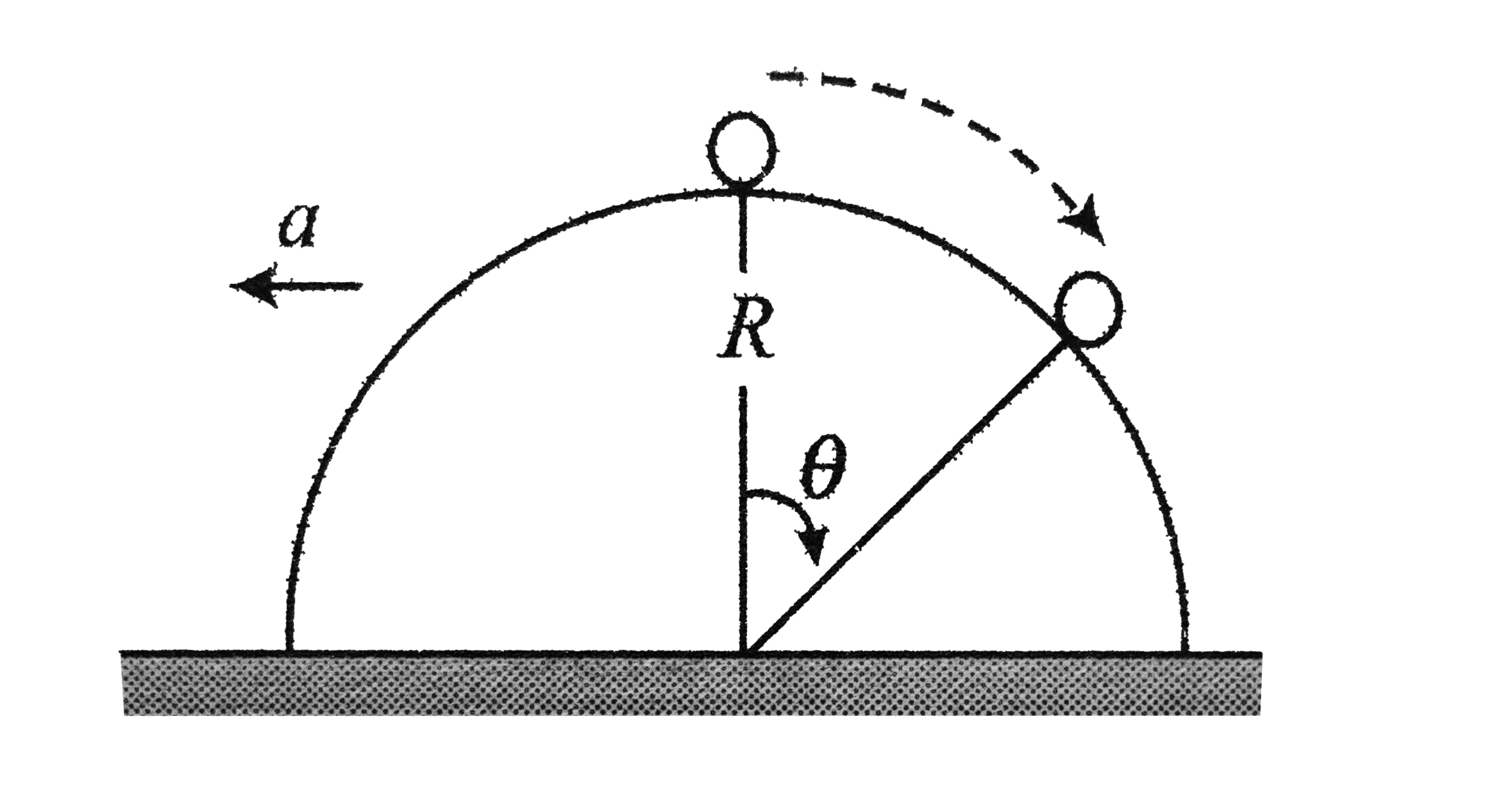 A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]
A√2R[g(1−sinθ)+aRcosθ]B√2R[g(1+cosθ)−aRsinθ]C√2R[g(1−cosθ)+aRsinθ]D√2R[g(1+sinθ)−aRcosθ]
From the top to a tower 100m in height a ball is dropped and at the same instant another ball is projeced veticall y upwards from the ground so that it just reaches the top of tower. At what height do the two balls pass one another ?
View SolutionA circular disc of radius 'R' is placed co-axially and horizontally inside and opaque hemispherical bowl of radius 'a', Fig. The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index μ and the near edge of the dise becomes just visible. How far below the top of the bowl is the disc placed ?
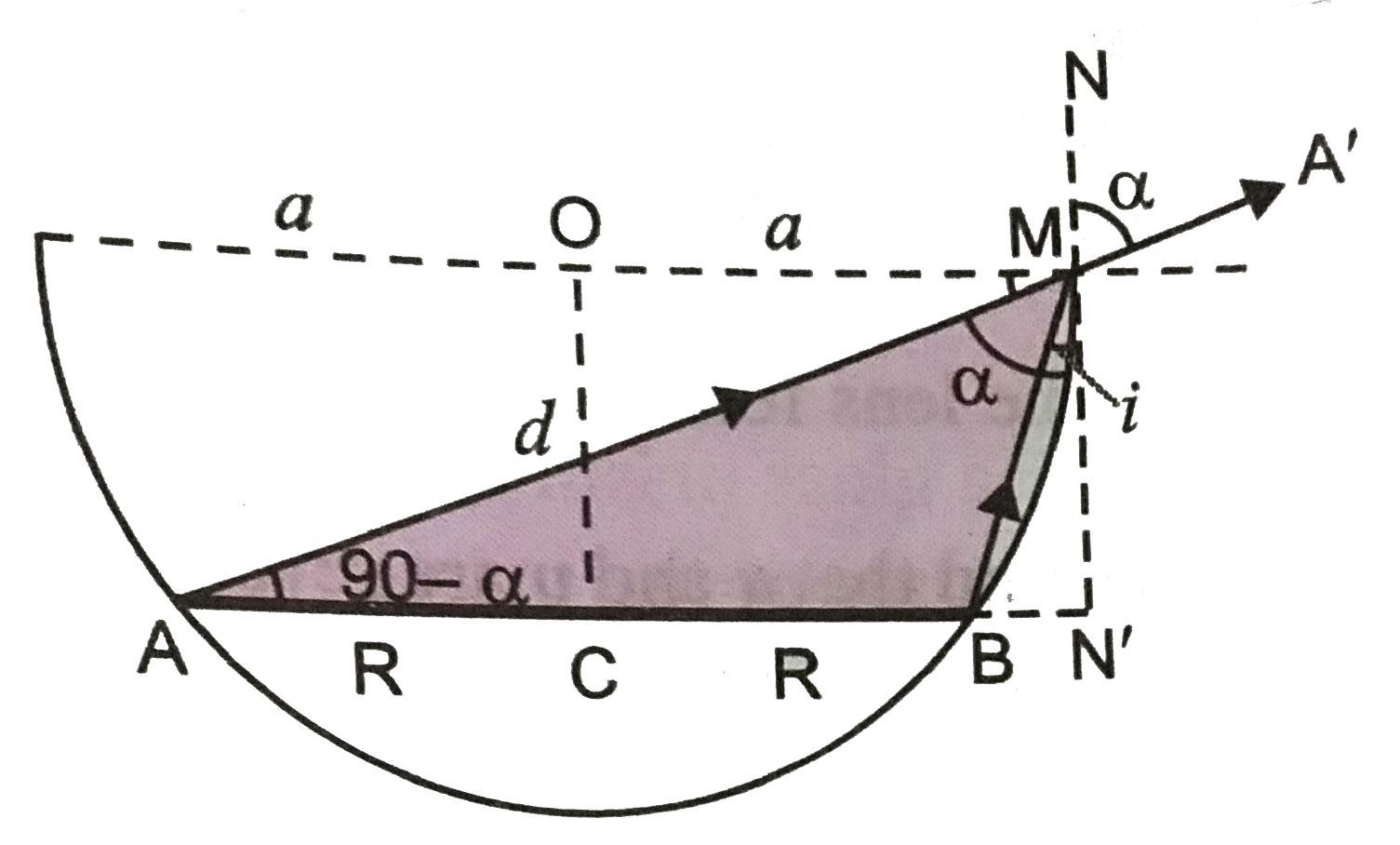 .
.
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
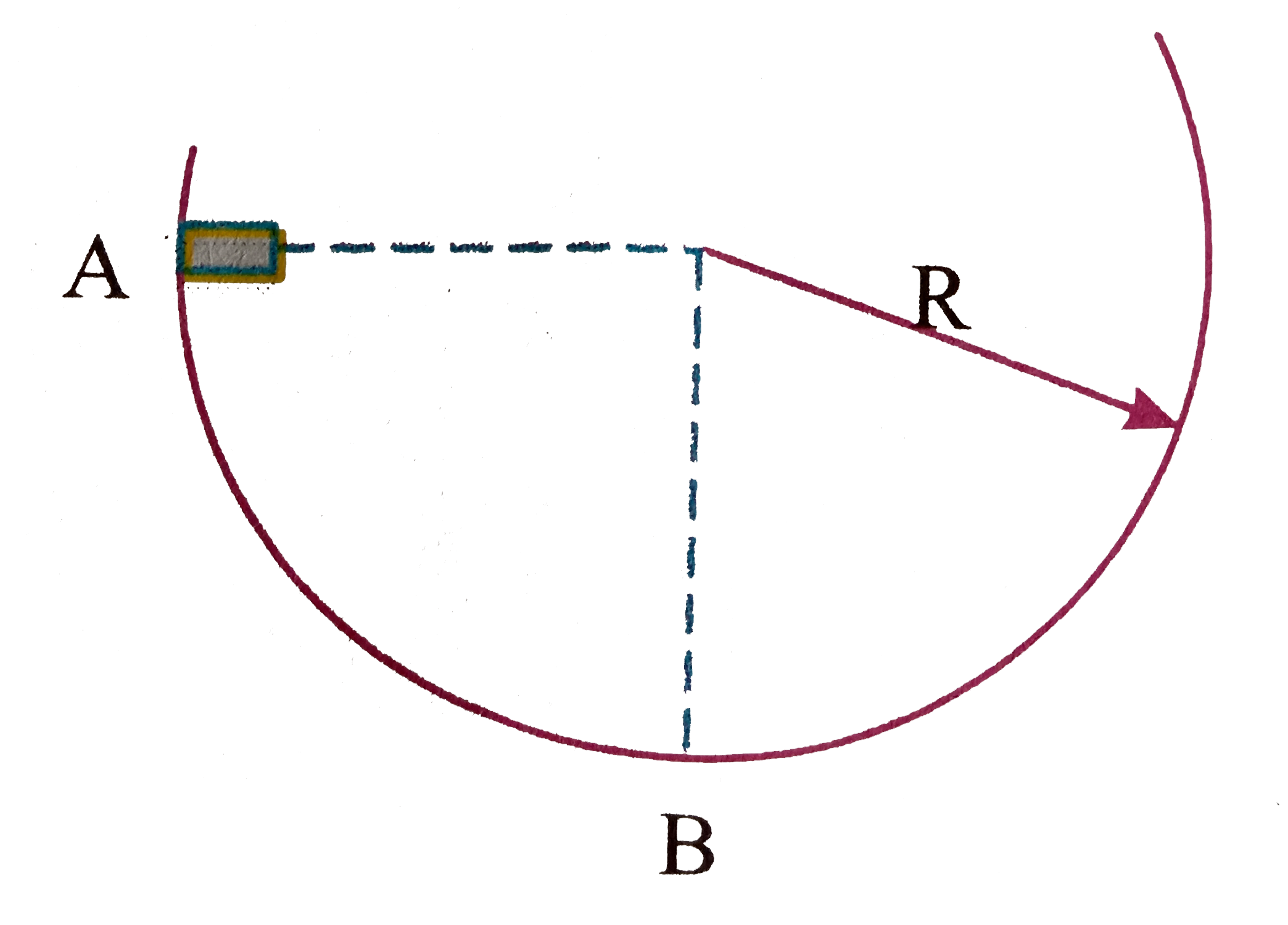
View SolutionA small ball is rolled with speed u from piont A along a smooth circular track as shown in figure. If x=3R, then

Determine the required speed u so that the ball returns to A, the point of projection after passing through C, the highest point.
View Solution
