A small ball of mass m is attached to a string of lengh R and moves in a vertical circle with a speed v m/s about a fixed point O as illustrated in fig. Find the tension in the string, when it makes an angle $θ$ with the vertical, in terms of $v, θ$ and g.

Video Solution

Text Solution

Verified by Experts

1. The speed of the ball is not uniform in this example as the gravitational force has a tangential component, at almost all points on the path.
2. It is not a uniform circular motion.
Calculations : Making the free body diagram, we see that the only forces acting on the ball are the weight and the tension exerted by the cord. Tension is always acting radialy inward. We need to resolve mg into a tangential component $m g sin θ$ and a radiual component $m g cos θ$ .
Apply Newton.s second law to the ball in the tangential direction,
$m g sin θ = m a_{t}$
$a_{t} = g sin θ$
Apply Newton.s second law to the forces acting on the ball in the radial direction.
$T - m g cos θ = \frac{m v^{2}}{R}$
$t = m g (\frac{v^{2}}{R g} + cos θ)$
Learn: It is importat to note that v in the expressio above varies for different positions as there is net tangential force acting on the particle.

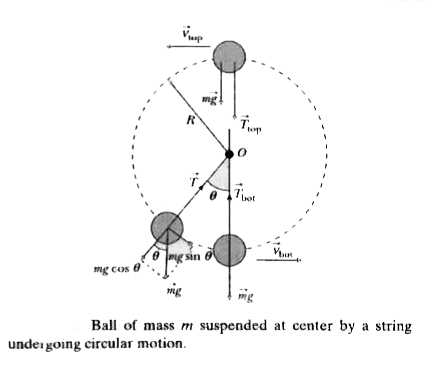
Case 1: What speed would the ball have at the top of the circle if the tension in the cord becomes zero at this point?
Keeping tension equal to zero in the abvoe expression, we get
$0 = m g (\frac{v_{top}^{2}}{R g} - 1) \Rightarrow v_{top} = \sqrt{g R}$
Case 2: What if the ball is given an initial velocity such that the speed at the top is less than this value? In this case the ball will not reach the top of the circle, as the tension in the string becomes zero to some lower point. The ball becomes a projectile as only force acting is gravity and ball has some oblique velocity.

Updated on:21/07/2023