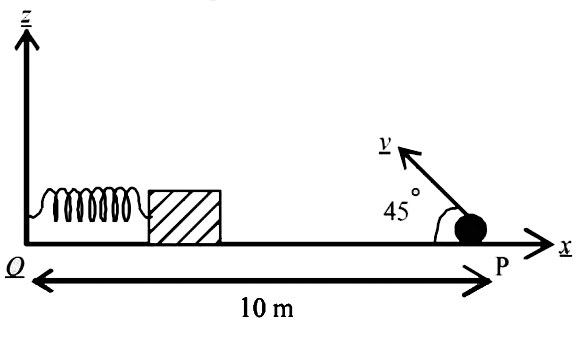
A small block is connected to one end of a massless spring of un - stretched length 4.9m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2m and released from rest at t=0. It then executes simple harmonic motion with angular frequency (ω)=(π/3)rad/s. Simultaneously at t=0, a small pebble is projected with speed (v) from point (P) at an angle of 45∘ as shown in the figure. Point (P) is at a horizontal distance of 10momO. If the pebble hits the block at t=1s, the value of (v) is (takeg=10m/s2).
 .
.
√50m/s
√51m/s
√52m/s
√53m/s
The correct Answer is:A
For block x=Asin(ωt+ϕ)
t=0, x=A⇒sinϕ=1⇒ϕ=π/2
x=Asin(ωt+ϕ)=Asin(ωt+π/2)=Acosωt
At t=1s, x=Acosω×1=0.2cos(2π3)=0.1m
Distance of block from O=4.9+0.1=5m
Range for pebble =10−5=5m
R=v2gsin(2×45∘)
5=v210⇒v=√50m/s
Topper's Solved these Questions
Similar Questions
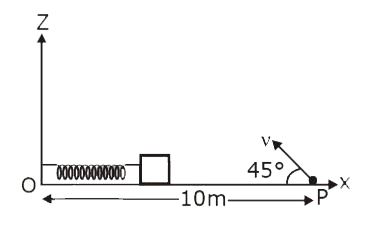
A small block is connected to one end of a massless spring of un-stretched length 4.9 m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2 m and released from rest at t = 0. It then executes simple harmonic motion with angular frequency ω=π3rad/s . Simultaneously at t = 0, a small pebble is projected with speed ν from point P at an angle of 45∘ as shown in the figure. Point P is at a horizontal distance of 10 m from O. If the pebble hits the block at t = 1s, the value of ν is (take g = 10 m/s2 )
View Solution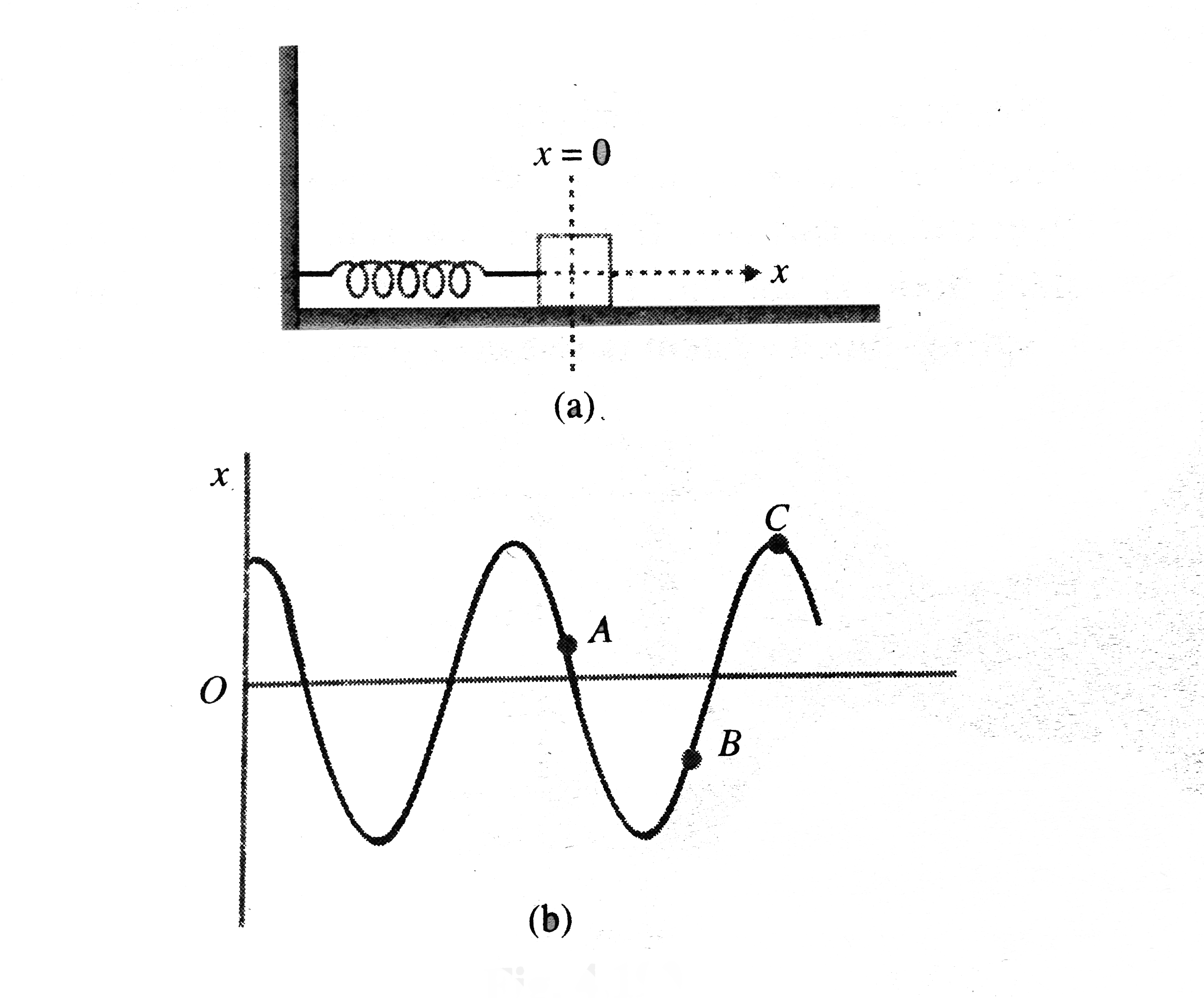
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Position of the block as a function of time can now be expressed as
View Solution
Knowledge Check
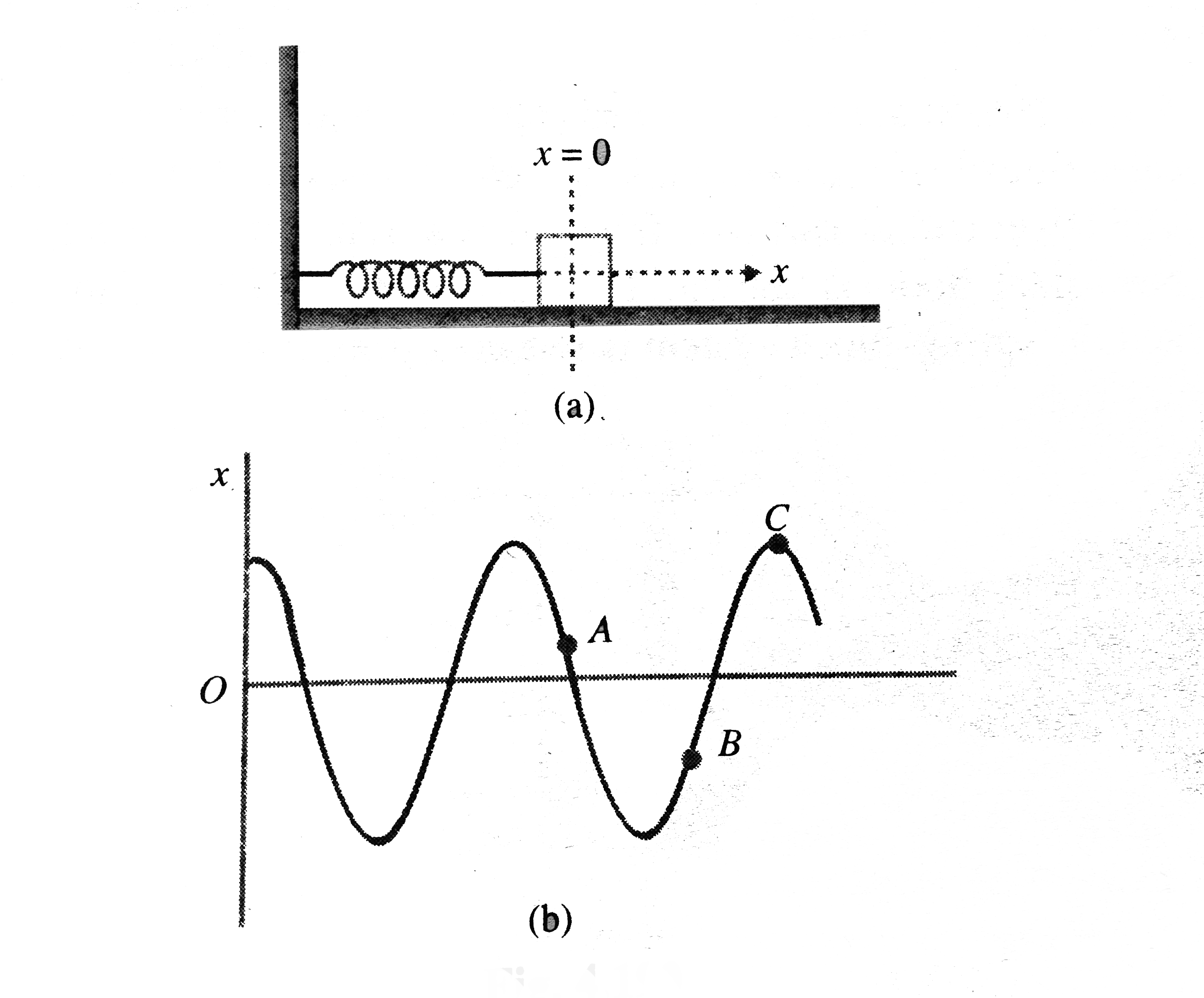
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x−direction∈decated∈Fig.Thepositiontime(x-t) graph of motion of the block is as shown in Fig.
Q. When the block is at position A on the graph, itsAposition and velocity both are negativeBposition is positive and velocity is negativeCposition is negative and velocity is positiveDposition and velocity both the positive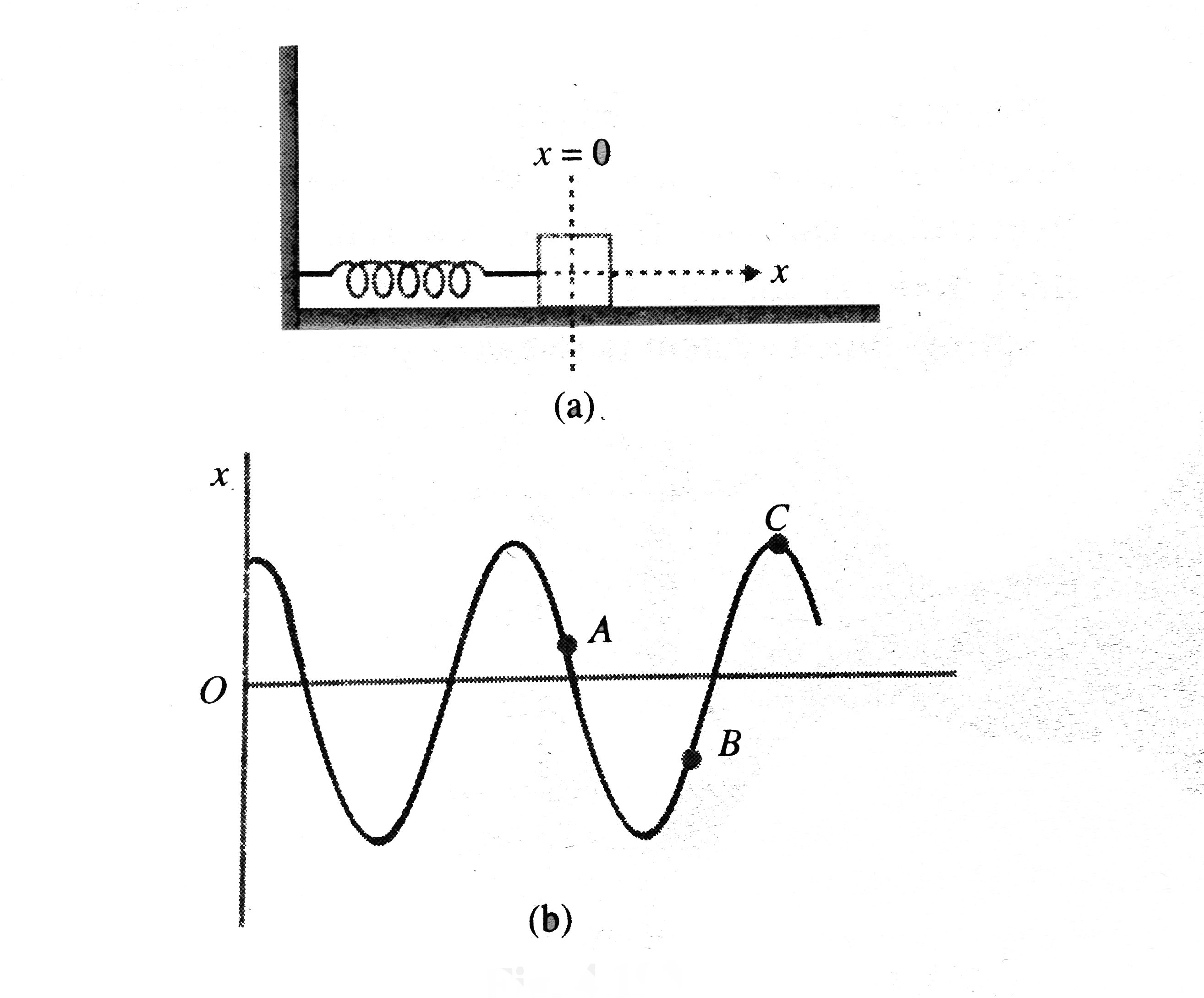
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Q. When the block is at position B on the graph its.Aposition and velocity both are positive.Bposition is positive and velocity is negativeCposition is negative and velocity is positiveDosition and velocity are negative.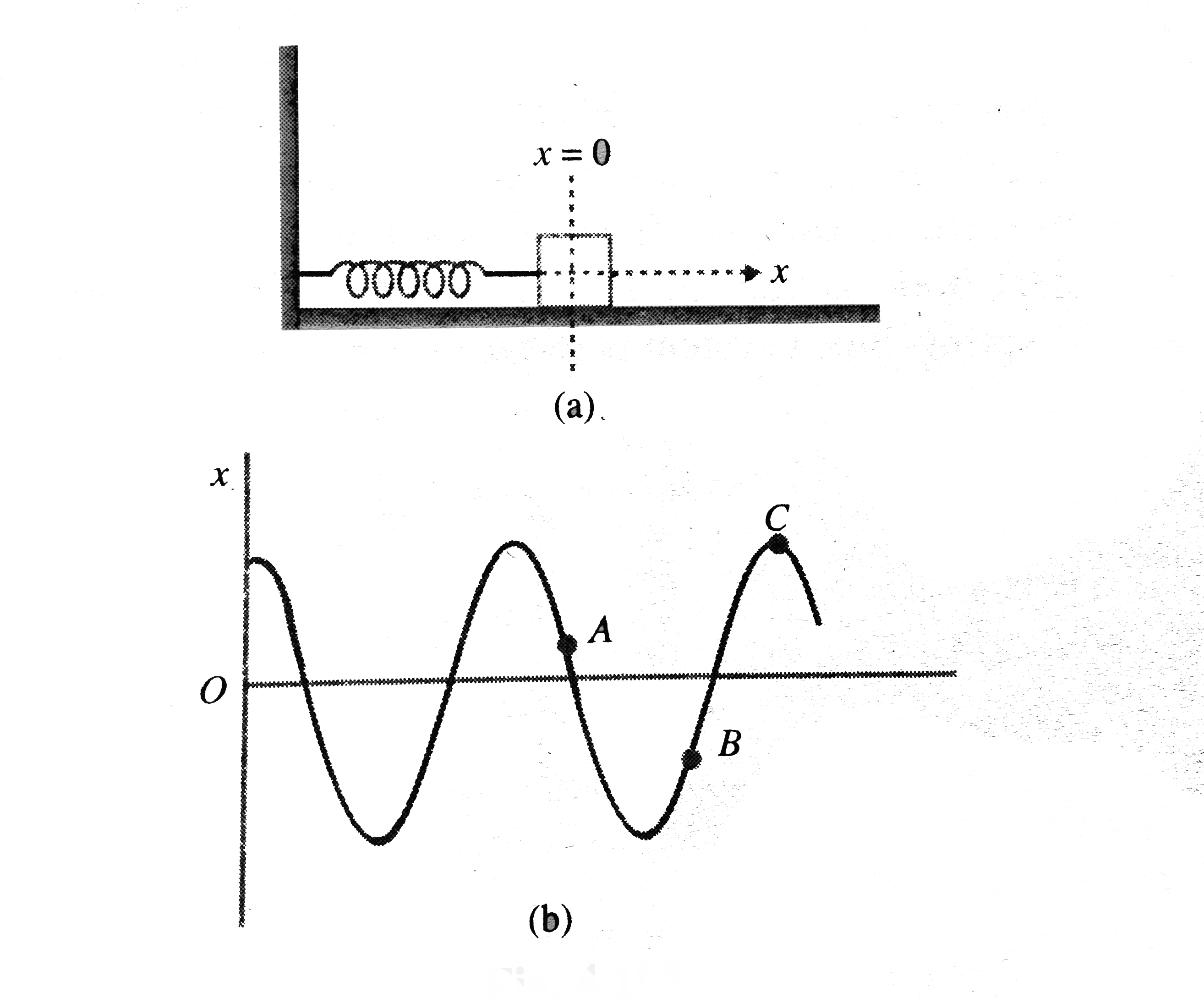
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
When the block is at position C on the graph, itsAvelocity is maximum and acceleration is zeroBvelocity is minimum and acceleration is zeroCvelocity is zero and acceleration is negativeDvelocity is zero and acceleration is positive.
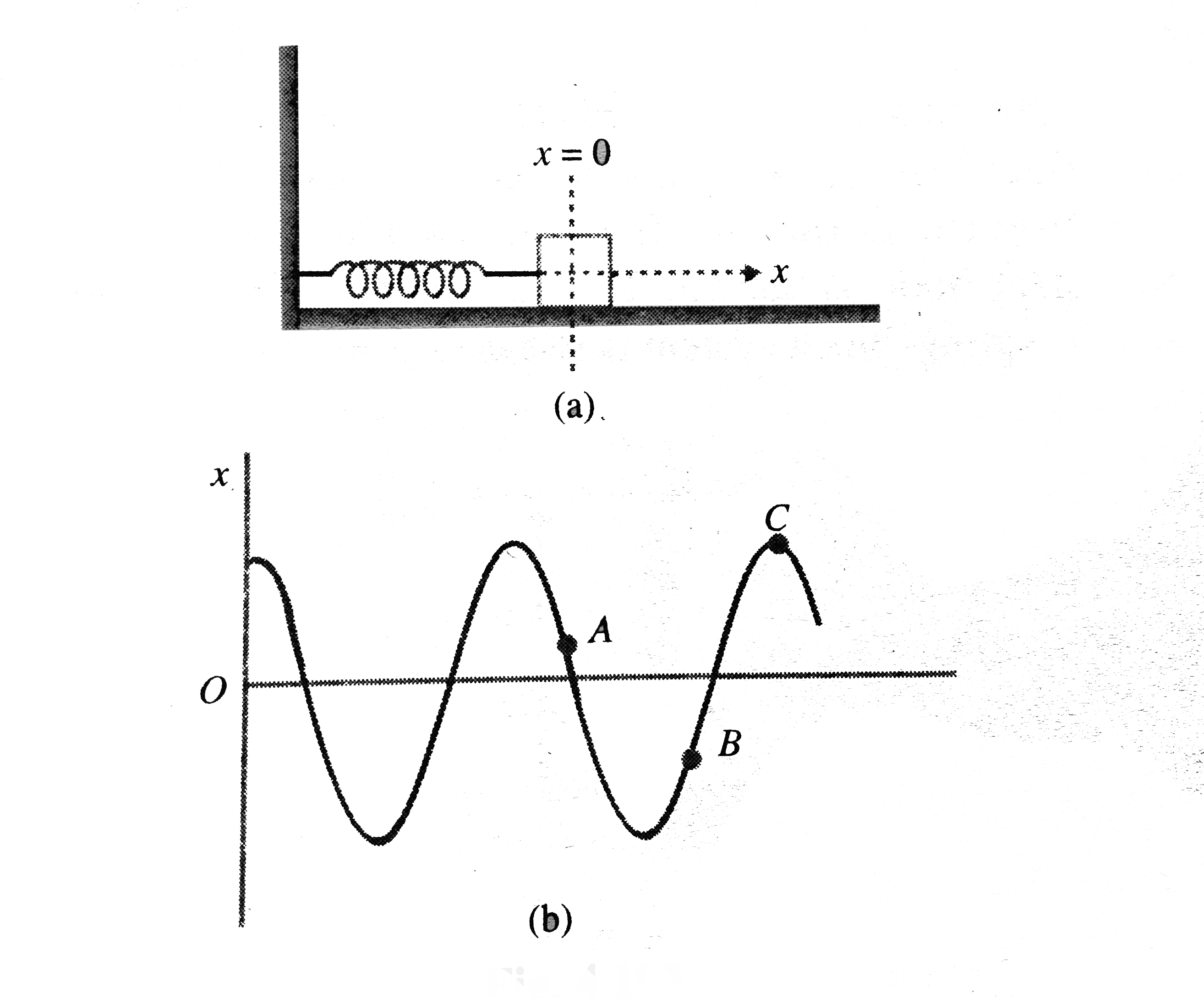
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed as
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA spring with one end attached to a mass and the other to a right support is stretched and released
View SolutionA 2.0 - kg block executes SHM while attached to a horizontal spring of spring constant 200N/m. The maximum speed of the block as it slides on a horizontal frictionless surface is 3.0m/s.
How long does the block take to complete 7.0 cycles of its motion?
View Solution