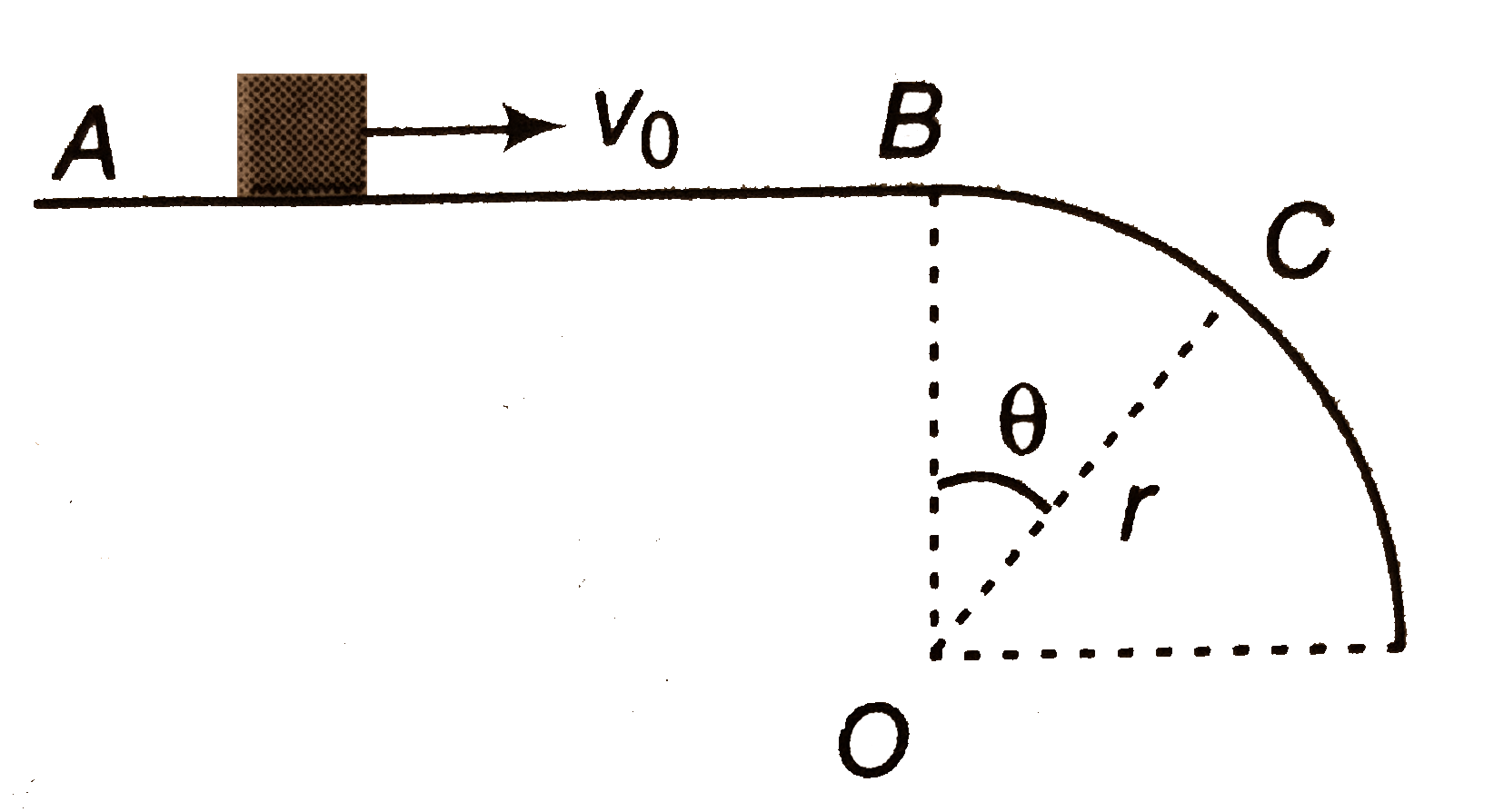
A small block slides with velocity 0.5√gr on the horizontal frictionless surface as shown in the figure. The block leaves the surface at point C . Calculate angle θ in the figure.
Cos−1(34)
Cos−1(49)
Cos−1(14)
Cos−1(54)
The correct Answer is:A, C, D
v2=v20+2gh=(0.5√gr)2+2gr(1−cosθ)
=(2.25gr−2grcosθ)
At the time of leaving contact, N=0
:. mgcosθ=mv2r=2.25mg−2mgcosθ
:. cosθ=2.253=34
:. θ=cos−1(3/4)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct
18 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Objective
14 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
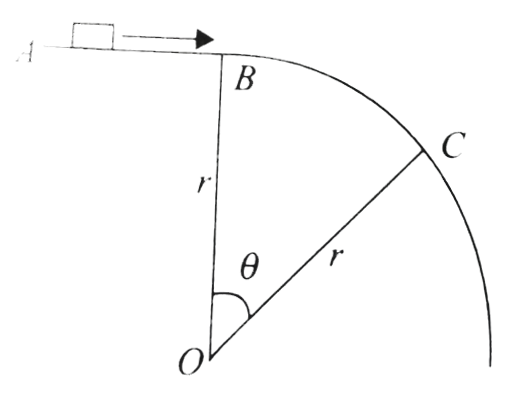
A small block slides with velocity v0=0.5√gr on the horizontal frictiohnless surface as shown in the fig. the block leaves the surface at point C. The angle θ in the figure is:
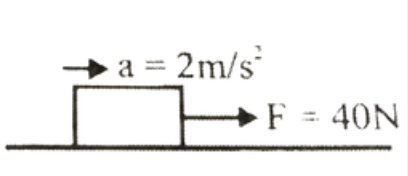
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
View SolutionA block of mass m slides along a frictionless surface as shown in the figure. If it is releases from rest from A what is its speed at B?

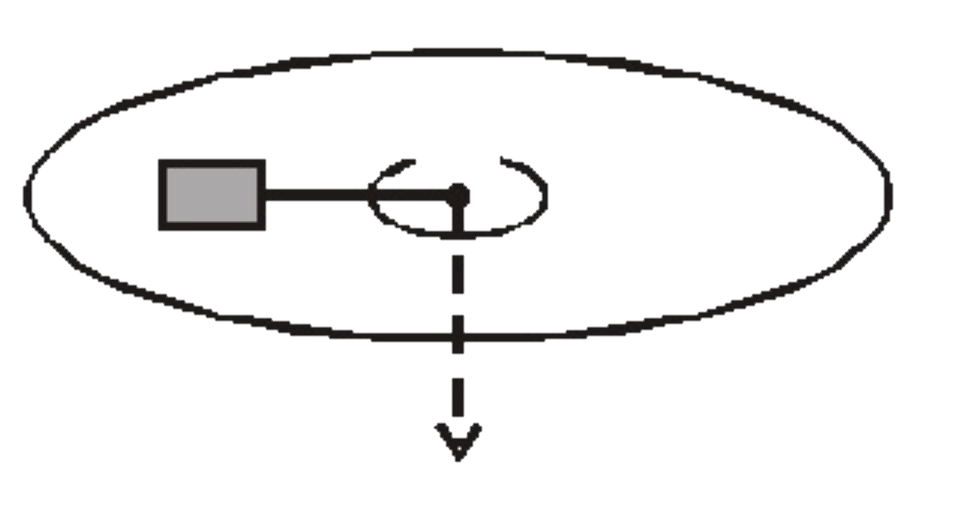
View SolutionA block of mass 0.1 kg is attached to a cord passing through a hole in a horizontal frictionless horizontal surface as shown in the figure. The block is originally revolving at a distance of 0.4 m from the hole, with an angular velocity of 2 rad s−1. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.2 m. Considering the block to be point mass, calculate the new angular velocity (in rad s−1)
View Solution
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal to
View SolutionA block of mass M rests on a rough horizontal surface as shown. Coefficient of friction between the block and the surface is μ. A force F=mg acting at angle θ with the vertical side of the block pulls it. In which of the following cases the block can be pulled along the surface?

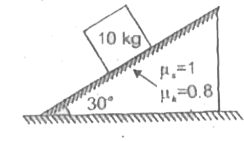
View SolutionA block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
View SolutionA small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
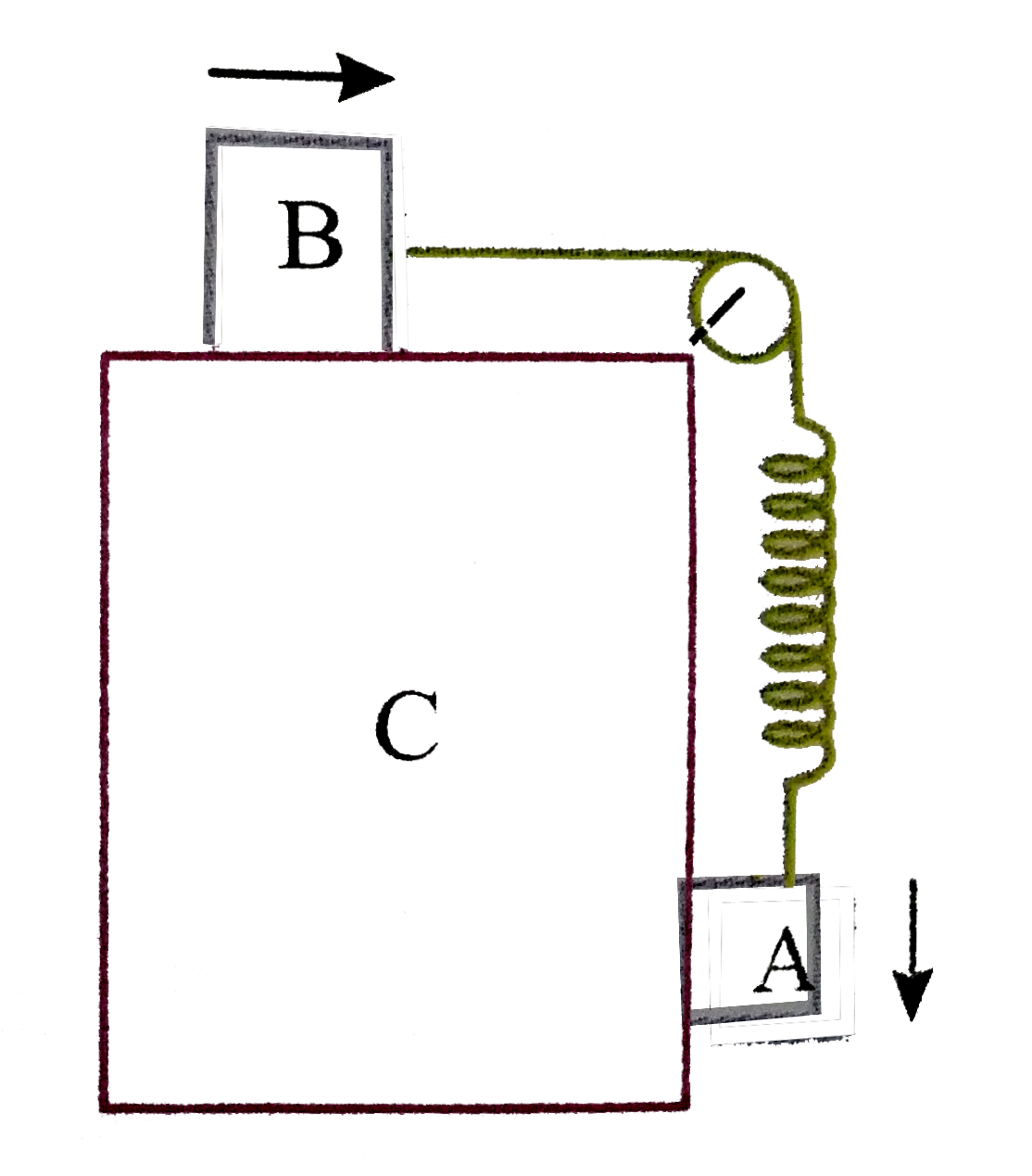
View SolutionTwo blocks A and B are connected to each other by a string and a spring , the string passes over a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed. The coefficient of friction between the surface and blocks is 0.5,K=2000N/m. If mass of A is 2kg calculate mass of B.
 .
.
View SolutionTwo blocks A and B are connected to each other by a string and a spring, the string passes over a frictionless pulley as shown in the figure. Block B slides over the horizontal top surface of a stationary block C and the block A slides along the vertical side of C, both with the same uniform speed. The coefficient of friction between the surfaces of blocks is 0.2. Force constant of the spring is 1960 newtons/m. If mass of block A is 2 kg. The mass of block B and the energy stored in the spring are _____ kg and _____ J.

View Solution